题目内容
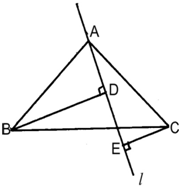 24、如图所示,已知在△ABC中,∠BAC=90°,AB=AC,l是过A点的直线,BD⊥l交直线l于点D,CE⊥l交直线l于点E.
24、如图所示,已知在△ABC中,∠BAC=90°,AB=AC,l是过A点的直线,BD⊥l交直线l于点D,CE⊥l交直线l于点E.(1)求证:△ABD≌△CAE.
(2)若BD=2.5cm,CE=0.8cm,求DE的长.
分析:根据垂直的定义与直角三角形的两个锐角互余的性质求得∠ABD+∠BAE=90°,∠BAE+∠AEC=90°,所以由等量代换知∠BAD=∠CAE;再由已知条件BD⊥AE,CE⊥AE,AB=AC,可以推知△ABD≌△CAE(ASA);
(2)根据(1)的结论可得:DE=AE-AD=BD-CE,从而可得出答案.
(2)根据(1)的结论可得:DE=AE-AD=BD-CE,从而可得出答案.
解答:解:(1)∠ABD+∠BAE=90°,∠BAE+∠AEC=90°,
∴∠BAD=∠CAE,
又∵BD⊥AE,CE⊥AE,AB=AC,
∴△ABD≌△CAE(ASA);
(2)由(1)的结论可得:DE=AE-AD=BD-CE=2.5-0.8=1.7cm.
∴∠BAD=∠CAE,
又∵BD⊥AE,CE⊥AE,AB=AC,
∴△ABD≌△CAE(ASA);
(2)由(1)的结论可得:DE=AE-AD=BD-CE=2.5-0.8=1.7cm.
点评:本题考查了全等三角形的判定与性质.解答该题时,围绕结论寻找全等三角形,运用全等三角形的性质判定对应线段相等.

练习册系列答案
相关题目
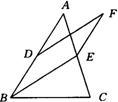 19、如图所示,已知在△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的关系,并说明理由.
19、如图所示,已知在△ABC中,D是AB的中点,E是AC上的点,且∠ABE=∠BAC,EF∥AB,DF∥BE,请猜想DF与AE有怎样的关系,并说明理由. 19、如图所示,已知在△ABC中,∠B=90°,点D、点E分别在BC和AB上.求证:AD2+CE2=AC2+DE2.
19、如图所示,已知在△ABC中,∠B=90°,点D、点E分别在BC和AB上.求证:AD2+CE2=AC2+DE2.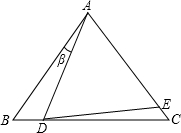 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)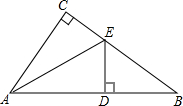 如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=
如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC=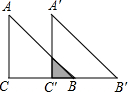 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.