题目内容
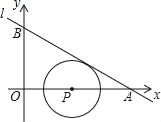
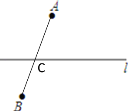
【题目】(1)如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并保留作图痕迹.

(探索)
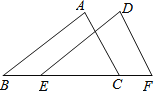
(2)如图,C、B两个村庄在一条笔直的马路的两端,村庄A在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置.
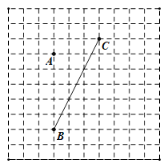
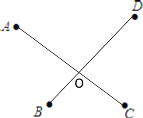
(3)如图,现有A、B、C、D四个村庄,如果要建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置.
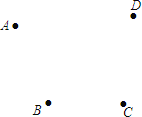
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)根据两点之间线段最短,连接AB,交l于点C即可;
(2)根据BO+CO=BC为定长,故需保证AO最小即可,根据垂线段最短,过点A作AO⊥BC于O即可;
(3)根据两点之间线段最短,故连接AC、BD交于点O即可.
解:(1)连接AB,交l于点C,此时AC+BC=AB,根据两点之间线段最短,AB即为AC+BC的最小值,如下图所示:点C即为所求;
(2)∵点O在BC上
∴BO+CO=BC
∴AO+BO+CO=AO+BC,而BC为定长,
∴当AO+BO+CO最小时,AO也最小
过点A作AO⊥BC于O,根据垂线段最短,此时AO最小,AO+BO+CO也最小,如下图所示:点O即为所求;
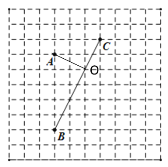
(3)根据两点之间线段最短,若使AO+CO最小,连接AC,点O应在线段AC上;若使BO+DO最小,连接BD,点O应在线段BD上,
∴点O应为AC和BD的交点
如下图所示:点O即为所求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目