题目内容
【题目】在△ABO中,若OA=OB=2,⊙O的半径为1,当∠AOB满足____________时,直线AB与⊙O相切;当∠AOB满足____________时,直线AB与⊙O相交;当∠AOB满足____________时,直线AB与⊙O相离.
【答案】∠AOB=120° 120°<∠AOB<180° 0°<∠AOB<120°
【解析】
当直线AB与圆相切时,AB边上的高等于圆的半径,从而求得∠AOB的度数,并以此为界限,完成另外两空.
解:过O作OC⊥AB于C,则∠AOC=1/2∠AOB.
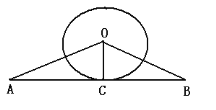
(1)当AB与⊙O相切时,有OC=r=1.
在Rt△AOC中,cos∠AOC=![]() ,
,
∴∠AOC=60°,
∴∠AOB=2∠AOC=120°.
(2)当AB与⊙O相交时有OC<r,
在Rt△AOC中,cos∠AOC=OC:OA,
∴60°<∠AOC<90°,
∴120°<∠AOB<180°.
(3)当AB与⊙O相离时,有OC>r,
在Rt△AOC中cos∠AOC=OC:OA,
∴0°<∠AOC<60°,
∴0°<∠AOB<120°.
故答案为:(1). ∠AOB=120° (2). 120°<∠AOB<180° (3). 0°<∠AOB<120°

练习册系列答案
相关题目