题目内容
如图,在正方形ABCD中, E是AB上一点,F是AD延长线上一点,且
DF=BE=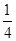 BC=1.
BC=1.
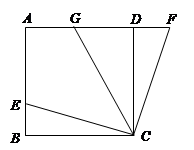
小题1:求证:CE=CF;
小题2:若G在AD上,连结GC,且∠GCE=45°,求∠GCF的度数
小题3:在(2)的条件下,求GC的长度.
DF=BE=
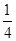 BC=1.
BC=1.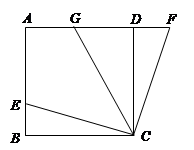
小题1:求证:CE=CF;
小题2:若G在AD上,连结GC,且∠GCE=45°,求∠GCF的度数
小题3:在(2)的条件下,求GC的长度.
小题1:∵ABCD是正方形
∴BC=CD ∠EBC=∠CDF=90°
∵DF=BE
∴△BCE≌△CDF
∴CE=CF(3分)
小题2:∵∠GCE=45°
∴∠BCE+∠GCD=45°
∵△BCE≌△CDF
∴∠BCE=∠DCF
∴∠GCF=∠DCF+∠GCD=∠BCE+∠GCD=45°(3分)
小题3:tan∠GCF=
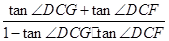 =1,
=1,tan∠GCD=
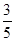
GD=CD tan∠GCD=
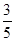
GC=
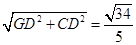 (4分)
(4分)(1)利用SAS证明△BCE≌△CDF;
(2)利用角的等量代换;
(3)利用正切定律。
(2)利用角的等量代换;
(3)利用正切定律。

练习册系列答案
相关题目

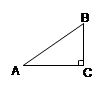
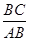





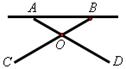
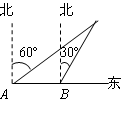
 ,∠AOC为( )
,∠AOC为( )
