题目内容
【题目】综合题
(1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.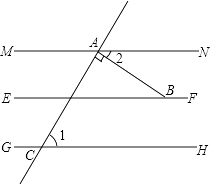
(2)计算: ![]() +
+ ![]() +|
+| ![]() ﹣2|﹣2.
﹣2|﹣2.
【答案】
(1)解:∵MN∥EF,GH∥EF,
∴MN∥GH,
∵∠1=70°,∠CAB=90°,
∴∠2=180°﹣∠1﹣∠CAB=20°,
∴∠ABF=180°﹣∠2=160°
(2)解:原式= ![]() ﹣
﹣ ![]() +2﹣
+2﹣ ![]() ﹣2
﹣2
=﹣ ![]()
【解析】利用平行线的性质及角的和差关系.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握实数的运算(先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算)的相关知识才是答题的关键.

练习册系列答案
相关题目
【题目】商场销售A、B两种商品,它们的进价和售价如表所示.
A商品 | B商品 | |
进价(元/件) | 30 | 40 |
售价(元/件) | 50 | 70 |
(1)若该商场购进A、B两种商品共60件,恰好用去2050元,求购进A、B两种商品各多少件?
(2)该商场第二次购买A、B两种商品,而B商品数量比A商品数量的2倍少6件,且购买总额不超过2840元,总利润不少于1900元.请你帮助该商场设计相应的进货方案;
(3)若一个星期该商场销售A、B两种商品的总利润恰好是140元,求销售A、B两种商品各多少件?