题目内容
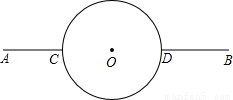
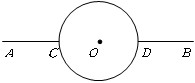
如图,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A,B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→
→线段DB,其中C,D在直线A
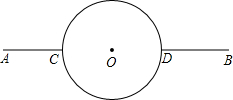
B上.请你找出最短的行走路线,并求出这条路线的长度.(
≈1.73,π≈3.14)
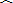 |
| CD |

B上.请你找出最短的行走路线,并求出这条路线的长度.(
| 3 |
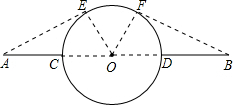
如图所示,分别过A、B两点作圆O的切线,切点为E,F两点.
则最短的行走路线是:
线段AE→
 |
| EF |
连接OC,OD,OE,OF(A,C,B,D,O在同一直线上).
∵∠AEO=90°,OE=15,OA=30
∴∠AOE=60°,AE=15
| 3 |
同理:∠FOB=60°,BF=15
| 3 |
∴∠EOF=60°
∴
 |
| EF |
| 1 |
| 6 |
∴AE+
 |
| EF |
| 3 |
答:最短的行走路线长约为67.6km.

练习册系列答案
相关题目

 B上.请你找出最短的行走路线,并求出这条路线的长度.(
B上.请你找出最短的行走路线,并求出这条路线的长度.(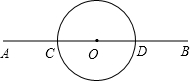 如图,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A、B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→弧CD→线段DB,其中C、D在直线AB上.则最短的行走路线的长度是
如图,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A、B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→弧CD→线段DB,其中C、D在直线AB上.则最短的行走路线的长度是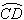 →线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度。
→线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度。
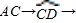 线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.(
线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.( ≈1.73,π≈3.14)
≈1.73,π≈3.14)