题目内容
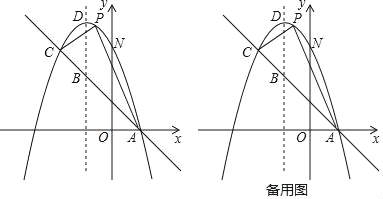
【题目】已知:![]() 为
为![]() 直径,点
直径,点![]() 为
为![]() 上一点,弦
上一点,弦![]() ,垂足为
,垂足为![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
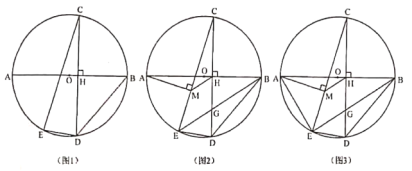
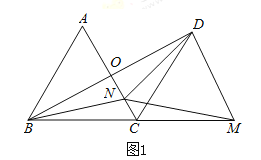
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
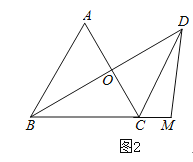
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)详见解析;(2)详见解析;(3)![]() 半径为
半径为![]() .
.
【解析】
(1)由AB为直径,CD⊥AB,得![]() ,从而∠CEB=∠BED=∠CDB,即可得到∠CED=2∠CDB,结合∠CDE=2∠CDB,即可求解;
,从而∠CEB=∠BED=∠CDB,即可得到∠CED=2∠CDB,结合∠CDE=2∠CDB,即可求解;
(2)由![]() 可得∠ACE=∠ABE,由AM⊥CE,CH⊥AB,可得∠AHC=∠AMC,则∠AHM=∠ACM,故∠AHM=∠ABE,即可求解;
可得∠ACE=∠ABE,由AM⊥CE,CH⊥AB,可得∠AHC=∠AMC,则∠AHM=∠ACM,故∠AHM=∠ABE,即可求解;
(3)证明△AEF≌△AEM(AAS)、△AFD≌△AMC(AAS)、△CGB∽△ECB,即可求解.
(1)∵![]() 为直径,
为直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
则∠AHM=∠ACM,
∴∠AHM=∠ABE,
∴MH∥BE;
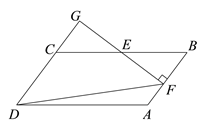
(3)连接![]() 、
、![]() 、
、![]() ,过
,过![]() 作
作![]() ,
,
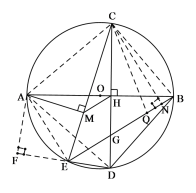
则![]() ,AE=AE,
,AE=AE,
∴![]() (AAS),
(AAS),
∴![]() ,EF=EM,
,EF=EM,
∵![]() 为直径,
为直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (HL) ,
(HL) ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
相似比![]() ,
,
∴设![]() ,
,![]() ,
,![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,
作![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 半径为
半径为![]() .
.

【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在![]() 之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A |
|
B |
|
C |
|
D |
|
E |
|
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在![]() 至
至![]() (不含
(不含![]() )的学生约有400人
)的学生约有400人
其中合理的说法是( )
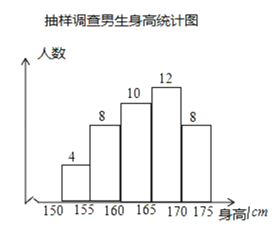
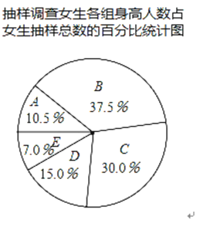
A.①②B.①④C.②④D.③④