题目内容
已知, BC∥OA,∠B=∠A=100°,试回答下列问题:
如图1所示,求证:OB∥AC.
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC ,并且OE平分∠BOF.则∠EOC的度数等于__ _____;(在横线上填上答案即可).
(3)在(2) 的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA度数等于 .(在横线上填上答案即可). 
(1)证明见试题解析;(2)400;(3)不变,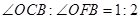 ;(4)600.
;(4)600.
解析试题分析:(1)根据等式性质及平行线的判定可以得到证明思路.(2)根据角平分线及观察图形知道
∠EOC=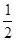 ∠BOC=400.(3)∠OFB与∠OCB实际上是三角形的外角与不相邻的内角的关系,再观察图形可知两直线平行内错角相等,角平分线分得的两个角相等,等量代换可得结论.(4)由∠OEB=∠OCA可以推出∠BOE=∠BCO=∠EOF=∠COF∠COA=200,从而∠OCA=600.
∠BOC=400.(3)∠OFB与∠OCB实际上是三角形的外角与不相邻的内角的关系,再观察图形可知两直线平行内错角相等,角平分线分得的两个角相等,等量代换可得结论.(4)由∠OEB=∠OCA可以推出∠BOE=∠BCO=∠EOF=∠COF∠COA=200,从而∠OCA=600.
试题解析:
(1)∵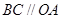 ∴
∴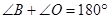
又∵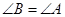 ∴
∴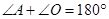
∴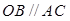
(2)40°
(3)∵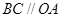
∴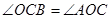
又∵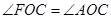
∴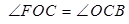
又∵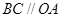 ∴
∴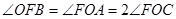
∴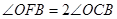
即
(4)60°
考点:1平行线的判定性质;2三角形的内外角关系;3角平分线性质;4等式性质.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目


 E、F分别在DC、AB延长线上.
E、F分别在DC、AB延长线上.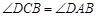 ,
, ,
, .
. 的大小.
的大小.




