题目内容
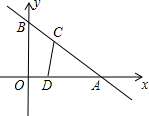 如图,已知一次函数y=-
如图,已知一次函数y=-| 3 | 4 |
(1)A点的坐标是(
(2)求AB的长;
(3)当t为何值时,△ACD和△AOB相似,并直接写出D点的坐标.
分析:(1)y=0代入解析式求得x的值,可得A的坐标,让x=0代入解析式求得y的值,可得B的坐标;
(2)由(1)得到两直角边长,利用勾股定理可得AB的长;
(3)利用相似的判定方法进行寻找等量关系,解出t即可得到答案.
(2)由(1)得到两直角边长,利用勾股定理可得AB的长;
(3)利用相似的判定方法进行寻找等量关系,解出t即可得到答案.
解答:解:(1)当y=0时,-
x+3=0,
解得x=4,
∴A(4,0),
同理B(0,3);
(2)由(1)知OA=4,OB=3,
∴AB=
=5;
(3)根据题意得
=
或
=
,
解得t=
或t=
,
此时分别对应D点的坐标为(
,0)或(
,0).
答(1)故填4,0,0,3;
(2)AB的长为5;
(3)当t分别为
,
时三角形相似,此时D的坐标分别为(
,0)或(
,0).
| 3 |
| 4 |
解得x=4,
∴A(4,0),
同理B(0,3);
(2)由(1)知OA=4,OB=3,
∴AB=
| 32+42 |
(3)根据题意得
| 5-t |
| 5 |
| t |
| 4 |
| 5-t |
| 4 |
| t |
| 5 |
解得t=
| 20 |
| 9 |
| 25 |
| 9 |
此时分别对应D点的坐标为(
| 16 |
| 9 |
| 11 |
| 9 |
答(1)故填4,0,0,3;
(2)AB的长为5;
(3)当t分别为
| 20 |
| 9 |
| 25 |
| 9 |
| 16 |
| 9 |
| 11 |
| 9 |
点评:本题考查了一次函数的综合应用;第3小问题中分类讨论是正确解答本题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数