题目内容
阅读下面解方程组的方法,然后回答有关问题:
解方程组 时,如果直接消元,那将是很繁琐的,若采用下面的解法则会简便许多.
时,如果直接消元,那将是很繁琐的,若采用下面的解法则会简便许多.
解:①-②,得2x+2y=2,即x+y=1③
③×16,得16x+16y=16④
②-④,得x=-1,从而y=2∴方程组的解为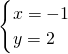
请你采用上述方法解方程组: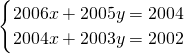
并猜测关于x、y的方程组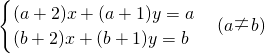 的解是什么?并利用方程组的解加以验证.
的解是什么?并利用方程组的解加以验证.
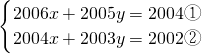
解:①-②,得2x+2y=2即x+y=1③,
③×2003,得2003x+2003y=2003④,
②-④得x=-1,从而y=2,
∴方程组得解为
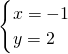 .
.猜想方程组
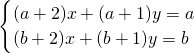 的解为
的解为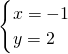 .
.检验:把x=-1,y=2代入(a+2)x+(a+1)y=a得:左边=a,右边=a,左边=右边;
把x=-1,y=2代入(b+2)x+(b+1)y=b得:左边=b,右边=b,左边=右边;
∴
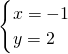 是方程组的解.
是方程组的解.分析:①-②求出x+y=1③,②-③×2003求出x的值,同理求出y的值;根据以上两方程组的特点和解的特点,即可写出答案,把方程组的解代入每个方程,只要左边=右边,就是方程组的解.
点评:本题考查了解二元一次方程组的应用,关键是培养学生的阅读能力和理解能力,能否根据已知得出规律也是解此题的关键之一,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
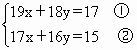
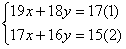 时,我们如果直接考虑消元,那将是很麻烦的,而采用下面的解法是轻而易举的。
时,我们如果直接考虑消元,那将是很麻烦的,而采用下面的解法是轻而易举的。 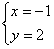
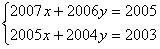
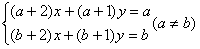 的解是什么?并利用方程组的解加以验证。
的解是什么?并利用方程组的解加以验证。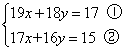 、阅读下面解方程组的方法,然后回答有关问题:
、阅读下面解方程组的方法,然后回答有关问题: