题目内容
函数y=-(x+5)2+7的对称轴是 ,顶点坐标是 ,图象开口向 ,当x 时,y随x 的增大而减小,当 时,函数y有最 值,是 .
【答案】分析:已知抛物线解析式为顶点式,可确定对称轴、顶点坐标,二次项系数为负数,可确定开口方向、增减性及最大值.
解答:解:∵y=-(x+5)2+7为抛物线的顶点式,
∴抛物线的对称轴是x=-5,顶点坐标是(-5,7),
图象开口向下,
当x>-5时,y随x 的增大而减小,
当=-5时,函数y有最大值,是7.
点评:本题考查了抛物线的顶点式与抛物线的性质之间的关系,关键是明确抛物线的顶点坐标及开口方向.
解答:解:∵y=-(x+5)2+7为抛物线的顶点式,
∴抛物线的对称轴是x=-5,顶点坐标是(-5,7),
图象开口向下,
当x>-5时,y随x 的增大而减小,
当=-5时,函数y有最大值,是7.
点评:本题考查了抛物线的顶点式与抛物线的性质之间的关系,关键是明确抛物线的顶点坐标及开口方向.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| ||
| x |
A、x≤
| ||
B、x>-
| ||
| C、x≠0 | ||
D、x<
|
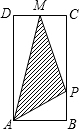 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )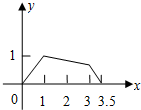


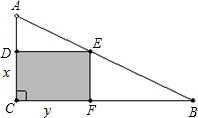 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.