题目内容
如图,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当动点Q到达点D时另一个动点P也随之停止运动.设运动的时间为t(秒).

(1)设△DPQ的面积为S,求S与t之间的函数关系式及t的取值范围;
(2)当t为何值时,以P、C、D、Q为顶点的四边形是平行四边形?

(1)设△DPQ的面积为S,求S与t之间的函数关系式及t的取值范围;
(2)当t为何值时,以P、C、D、Q为顶点的四边形是平行四边形?
(1)s=-6t+96 (0≤t≤16)
当 或
或 时以P、C、D、Q为顶点的四边形是平行四边形
时以P、C、D、Q为顶点的四边形是平行四边形
当
 或
或 时以P、C、D、Q为顶点的四边形是平行四边形
时以P、C、D、Q为顶点的四边形是平行四边形试题分析:

(1)S=
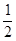 QD×AB=
QD×AB=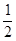 ×(16-t)×12=96-6t
×(16-t)×12=96-6t当P到达C点时,用时10.5s。Q到达D点用时16s
则0≤t≤10.5
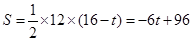 3分
3分(0≤t≤16) 4分
(2)要使以P、C、D、Q为顶点的四边形是平行四边形
∵已有QD//PC
∴考虑两种情况
① P在线段BC上,0≤t<10.5,PQ//CD,则有
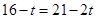
得
 7分
7分 ② P在BC延长上,10.5<t≤16,QC//DP,则有
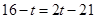
得
 10分
10分 综上,当
 或
或 时以P、C、D、Q为顶点的四边形是平行四边形.
时以P、C、D、Q为顶点的四边形是平行四边形.点评:此题是动点问题,难度适中,动点问题一般分:一是运动后研究其位置或图形形状的变化,二是运动后研究其函数模型的建立。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 的图象交于A(1,4)B(4,n)两点,与
的图象交于A(1,4)B(4,n)两点,与 轴交于D点,AC⊥
轴交于D点,AC⊥
 上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为
上的一点,过点M作x轴、y轴的垂线,分别交直线y=-2x+m于D、C两点,若直线y=-2x+m与y轴交于点A,与x轴相交于点B.则AD·BC的值为 
 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.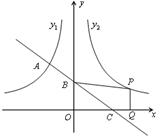
 (x>0)的图象与
(x>0)的图象与 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在 ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
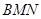 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与
 由直线
由直线 :
: 沿
沿 轴向右平移9个单位得到,则直线
轴向右平移9个单位得到,则直线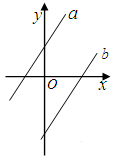
 的图象与
的图象与 轴的交点在
轴的交点在 轴的上方,则
轴的上方,则 的取值范围为 .
的取值范围为 . 与函数
与函数 在同一坐标系中的大致图象是下图中的 ( )
在同一坐标系中的大致图象是下图中的 ( )