题目内容
如图,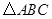 为直角三角形,
为直角三角形,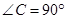 ,
,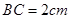 ,
,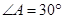 ;四边形
;四边形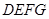 为矩形,
为矩形, ,
,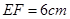 ,且点
,且点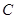 、
、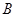 、
、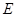 、
、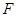 在同一条直线上,点
在同一条直线上,点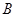 与点
与点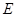 重合.
重合.
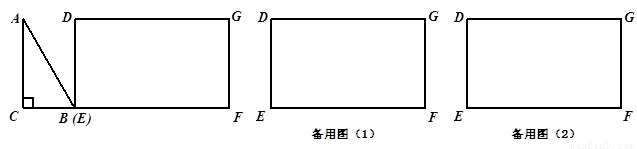
1.(1)求边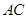 的长;
的长;
2.(2)将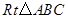 以每秒
以每秒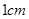 的速度沿矩形
的速度沿矩形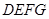 的边
的边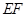 向右平移,当点
向右平移,当点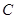 与点
与点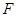 重合时停止移动,设
重合时停止移动,设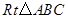 与矩形
与矩形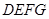 重叠部分的面积为
重叠部分的面积为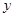 ,请求出重叠部分的面积
,请求出重叠部分的面积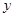 (
(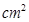 )与移动时间
)与移动时间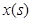 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);
3.(3)在(2)的基础上,当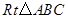 移动至重叠部分的面积为
移动至重叠部分的面积为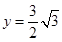
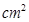 时,将
时,将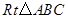 沿边
沿边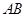 向上翻折,得到
向上翻折,得到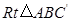 ,请求出
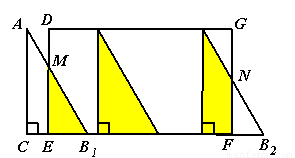
,请求出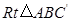 与矩形
与矩形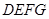 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
【答案】
1.
(1)∵ ,
,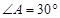 ,
,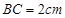
∴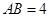 ,
,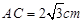 . ………………………………………4分
. ………………………………………4分
2.(2)①当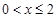 时,
时,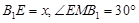
∴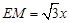 ,∴
,∴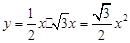 . …………………………6分
. …………………………6分
②当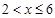 时,
时,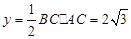 .…………………………7分
.…………………………7分
③当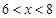 时,
时,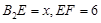 ,∴
,∴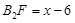 ,
,
在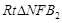 中,
中,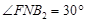 ,
,
∴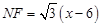 ,∴
,∴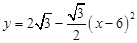 .………………………8分
.………………………8分
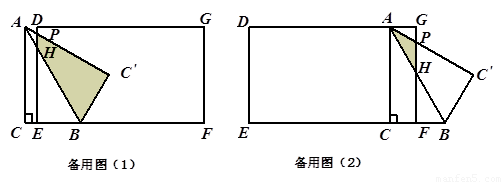
3.(3)①当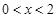 ,且
,且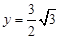 时,
时,
即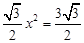 ,解得
,解得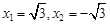 (不合题意,舍去).
(不合题意,舍去).
∴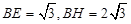 .
.
由翻折的性质,得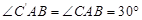 ,
,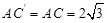 ,
,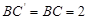 .
.
∵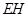 ∥
∥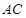 ,∴
,∴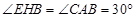
∵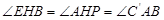 ,
,
∴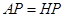
∴重叠部分的周长=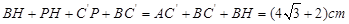
………………10分
②解法与①类似,当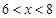 ,且
,且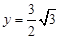 时,
时,
即 ,解得
,解得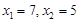 (不合题意,舍去).
(不合题意,舍去).
重叠部分的周长=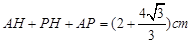 .
.
∴当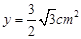 时,重叠部分的周长为
时,重叠部分的周长为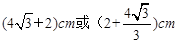 .…12分
.…12分
【解析】略

练习册系列答案
相关题目
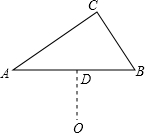 已知,如图△ABC为直角三角形,且∠C=90°,点D是AB的中点,OD⊥AB,并且
已知,如图△ABC为直角三角形,且∠C=90°,点D是AB的中点,OD⊥AB,并且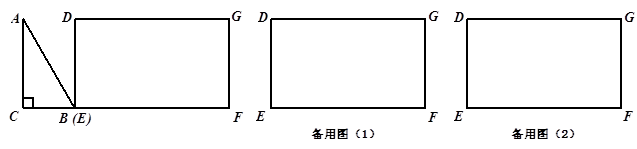
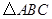 为直角三角形,
为直角三角形,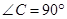 ,
, ,
,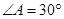 ;四边形
;四边形 为矩形,
为矩形,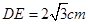 ,
,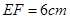 ,且点
,且点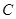 、
、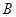 、
、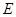 、
、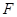 在同一条直线上,点
在同一条直线上,点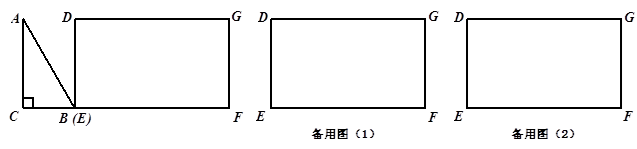
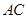 的长;
的长;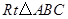 以每秒
以每秒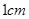 的速度沿矩形
的速度沿矩形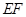 向右平移,当点
向右平移,当点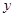 ,请求出重叠部分的面积
,请求出重叠部分的面积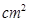 )与移动时间
)与移动时间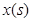 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);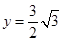
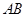 向上翻折,得到
向上翻折,得到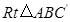 ,请求出
,请求出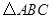 为直角三角形,
为直角三角形,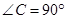 ,
,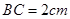 ,
,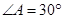 ;四边形
;四边形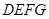 为矩形,
为矩形,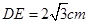 ,
,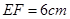 ,且点
,且点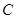 、
、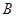 、
、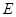 、
、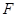 在同一条直线上,点
在同一条直线上,点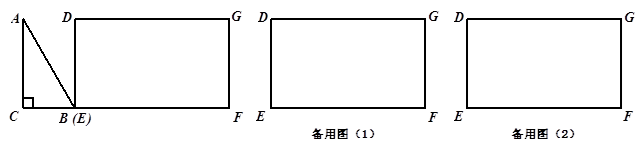
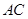 的长;
的长;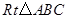 以每秒
以每秒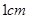 的速度沿矩形
的速度沿矩形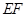 向右平移,当点
向右平移,当点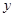 ,请求出重叠部分的面积
,请求出重叠部分的面积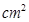 )与移动时间
)与移动时间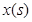 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);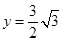
 向上翻折,得到
向上翻折,得到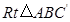 ,请求出
,请求出