题目内容
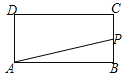
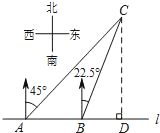
【题目】如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km，从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为_____km（精确到0.1）．
【答案】3.4．
【解析】分析: 根据题意在CD上取一点E，使BD=DE，设BD=DE=x，则由AD与CD的关系和勾股定理可求得x，从而可求得CD的长．
详解: 在CD上取一点E，使BD=DE，设BD=DE=x．
∵BD=DE，
∴∠EBD=45°，
由题意可得∠CAD=45°，
∴AD=DC，
∵从B测得船C在北偏东22.5°的方向，
∴∠BCE=∠CBE=22.5°，
∴BE=EC，
∵AB=AD﹣BD=2km，
∴EC=BE=DC﹣DE=2km，
∵BD=DE=x，
∴CE=BE=
x，
∴2+x=x+x，
解得x=．
∴DC=（2+）≈3.4（km）
故答案为3.4．
点睛: 此题主要考查了解直角三角形的应用，得出BE=EC=2是解题关键．
导学与测试系列答案
新非凡教辅冲刺100分系列答案
【题目】观察理解，并解决问题.
问题情境：如图所示，用一些相同的小正方形，拼在一起，排成如下的一些大正方形：
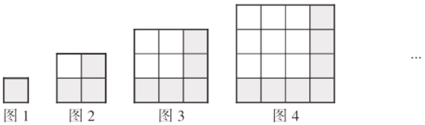
问题解决：（1）完成下表：
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
（2）根据图形规律推测：
______（用含
的代数式表示）
（3）像（1），（2）这样，根据某类事物的部分对象具有的某种性质，推出这类事物的所有对象具有的这种性质的推理，叫做归纳推理.对于科学的发现，归纳推理是十分有用的，通过观察、实验，对有限个对象的性质作归纳整理，提出对某类事物带有规律性的猜测，是科学研究的基本方法.请观察下列等式的规律：第一个等式：
；第二个等式：
；第三个等式：
；…猜想并直接写出第个等式.（用含的代数式表示）
