题目内容
【题目】如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点. 
(1)求证:EF是⊙O的切线;
(2)求AE的长.
【答案】
(1)证明:∵CD为直径,
∴∠DBC=90°,
∴BD⊥BC,
∵四边形OABC是平行四边形,
∴AO∥BC,
∴BD⊥OA,
∵EF∥BD,
∴OA⊥EF,
∴EF是⊙O的切线;
(2)解:连接OB,如图,
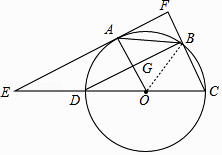
∵四边形OABC是平行四边形,
∴OA=BC,
而OB=OC=OA,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠C=60°,
∴∠AOE=∠C=60°,
在Rt△OAE中,∵tan∠AOE= ![]() ,
,
∴AE=3tan60°=3 ![]() .
.
【解析】(1)利用圆周角定理得到∠DBC=90°,再利用平行四边形的性质得AO∥BC,所以BD⊥OA,加上EF∥BD,所以OA⊥EF,于是根据切线的判定定理可得到EF是⊙O的切线;(2)连接OB,如图,利用平行四边形的性质得OA=BC,则OB=OC=BC,于是可判断△OBC为等边三角形,所以∠C=60°,易得∠AOE=∠C=60°,然后在Rt△OAE中利用正切的定义可求出AE的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根;
其中正确的有 . (填正确结论的序号)




