题目内容
【题目】如图所示,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=2∠AOC,求∠DOF. 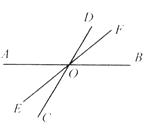
【答案】解:设∠AOC=x°,则∠BOC=(2x)°. 因为∠AOC与∠BOC是邻补角,所以∠AOC+∠BOC=180°
所以x+2x=180
解得x=60
所以∠AOC=60°.因为∠DOF与∠EOC是对顶角,
所以∠DOF=∠EOC=∠AOC-∠AOE=60°-40°=20°
【解析】图形中∠BOC与∠AOC互为邻补角,结合已知条件:∠BOC=2∠AOC,则可求出∠AOC,要求∠DOF只需求它的对顶角∠EOC即可,本题可用方程求解.
【考点精析】本题主要考查了对顶角和邻补角的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个才能正确解答此题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目