题目内容
如图,某中学有一块长为a m、宽为b m的矩形场地,计划在该场地上修筑宽都为2m的两条互相垂直的道路,余下的4块矩形小场地建成草坪.
(1)请分别写出每条道路的面积(用含a或含b的代数式表示).
(2)已知a∶b=2∶1,并且4块草坪的面积之和为312m2,试求原来矩形场地的长与宽各为多少?
(3)在(2)的条件下,为进一步美化校园,根据实际情况,学校决定对整个矩形场地作如下设计(要求同时符合下述两个条件):
条件①:在每块草坪上各修建一个面积尽可能大的菱形花圃(花圃各边必须分别与所在草坪的对角线平行),并且其中有两个花圃的面积之差为13m2;
条件②:整个矩形场地(包括道路、草坪、花圃)为轴对称图形.
请你画出符合上述设计方案的一种草图(不必说明画法与根据),并求出每个菱形花圃的面积.

答案:
解析:
解析:
|
解:(1)这两条道路的面积分别为2a m2与2b m2. (2)设b=x m,a=2x m,依题意得 x·2x-(2x+4x-4)=312.整理得x2-3x-154=0, 解得x1=14,x2=-11(舍去).∴b=14,a=2x=28. 即矩形的长为28m,宽为14m. (3)符合设计方案的一种草图如图(1)所示,其中4个菱形花圃中,第1个与第2个,第3个与第4个花圃的面积分别相等. 设AE=x,则FB=14-2-x=(12-x)m,AG= 依题意得 ∴大菱形花圃面积为 (注:其他符合设计方案的3种花圃见下面图(1)、图(2)、图(3),同上法仍可求得大、小花圃的面积分别为45.5m2与32.5m2)
|

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
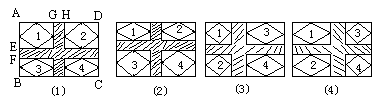
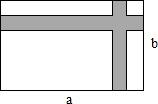
 某中学有一块长a米、宽b米的矩形场地.计划建如图的人行道(阴影部分),道宽为2米,余下部分建成草坪,已知a:b=2:1,并且草坪的面积为312米3,求原来矩形场地的长和宽各为多少米?
某中学有一块长a米、宽b米的矩形场地.计划建如图的人行道(阴影部分),道宽为2米,余下部分建成草坪,已知a:b=2:1,并且草坪的面积为312米3,求原来矩形场地的长和宽各为多少米?
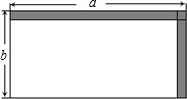 某中学有一块长a米、宽b米的矩形场地.计划建如图的人行道(阴影部分),道宽为2米,余下部分建成草坪,已知a:b=2:1,并且草坪的面积为312米3,求原来矩形场地的长和宽各为多少米?
某中学有一块长a米、宽b米的矩形场地.计划建如图的人行道(阴影部分),道宽为2米,余下部分建成草坪,已知a:b=2:1,并且草坪的面积为312米3,求原来矩形场地的长和宽各为多少米?