题目内容
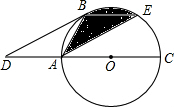 点D是⊙O的直径CA延长线上一点,点B在⊙O上,A是OD的中点,且AB=AD.
点D是⊙O的直径CA延长线上一点,点B在⊙O上,A是OD的中点,且AB=AD.(1)求证:BD是⊙O的切线.
(2)如果⊙O的半径为1,弦AE∥BD,cos∠AEB=
| ||
| 2 |
分析:(1)根据已知求出AB=AD=OA,推出∠DBO=90°,根据切线判定推出即可;
(2)先证明△ABD≌△EOD,将阴影部分的面积转化为扇形OBE的面积.
(2)先证明△ABD≌△EOD,将阴影部分的面积转化为扇形OBE的面积.
解答:(1)证明: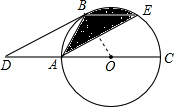 连接OB,
连接OB,
∵AC是⊙O直径,
∴OA=OC,
∵AB=AD,A为OD中点,
∴AB=AD=OA,
∴∠DBO=90°,
∴OB⊥DB,
∵OB为半径,
∴BD是⊙O切线;
(2)解: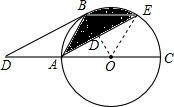 连接OE,OB,
连接OE,OB,
∵∠DBO=90°,AE∥BD,
∴∠ADO=90°,
∵AB=AD=OA,
∴AB=OE,
∴△ABD≌△EOD,
∴S阴影=S扇形OBE=
=
.
 连接OB,
连接OB,∵AC是⊙O直径,
∴OA=OC,
∵AB=AD,A为OD中点,
∴AB=AD=OA,
∴∠DBO=90°,
∴OB⊥DB,
∵OB为半径,
∴BD是⊙O切线;
(2)解:
 连接OE,OB,
连接OE,OB,∵∠DBO=90°,AE∥BD,
∴∠ADO=90°,
∵AB=AD=OA,
∴AB=OE,
∴△ABD≌△EOD,
∴S阴影=S扇形OBE=
| 60π×12 |
| 360 |
| π |
| 6 |
点评:本题考查了切线的判定,等腰三角形的性质,直角三角形的判定,垂径定理,圆周角定理,特殊角的三角函数值,三角形的面积,扇形的面积,弓形的面积等知识点的综合运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.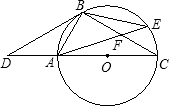 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. 点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.
点D是⊙O的直径CA延长线上一点,点B在⊙O上,BD是⊙O的切线,且AB=AD.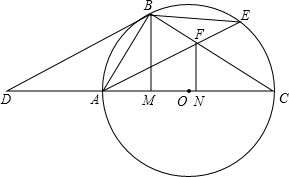 =30°.
=30°.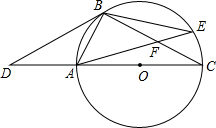 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.