题目内容
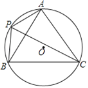
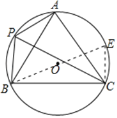
【题目】如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状,并证明你的结论;
(2)若BC的长为6,求⊙O的半径.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)根据圆周角定理得到∠ABC=∠APC=60°,∠CAB=∠CPB=60°,根据等边三角形的判定定理证明;
(2)延长BO交⊙O于E,连接CE,根据圆周角定理得到∠E=∠BAC=60°,根据正弦的概念计算即可.
解:(1)△ABC是等边三角形,
理由如下:由圆周角定理得,
∠ABC=∠APC=60°,∠CAB=∠CPB=60°,
∴△ABC是等边三角形;
(2)延长BO交⊙O于E,连接CE,
由圆周角定理得,∠E=∠BAC=60°,
∴BE=![]() ,
,
∴⊙O的半径为2![]() .
.

练习册系列答案
相关题目
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()