题目内容
若a、b、c是△ABC中∠A、∠B、∠C的对边,抛物线y=x2-2ax+b2交x轴于M(a+c,0),则△ABC是
- A.等腰三角形
- B.等边三角形
- C.直角三角形
- D.不确定
C
分析:抛物线y=x2-2ax+b2与x轴于M(a+c,0),把y=0代入抛物先的解析式,利用求根公式求出x的值即可求出a、b、c的关系式,进而可判断出三角形的形状.
解答:∵抛物线y=x2-2ax+b2交x轴于M(a+c,0),
∴当y=0时,x=a+c,
把y=0代入抛物线y=x2-2ax+b2交得,抛物线0=x2-2ax+b2,
解得,x= =a±
=a±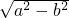 ,
,
∵a、b、c是△ABC中∠A、∠B、∠C的对边,
∴a>0,b>0,c>0,
∴a+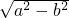 =a+c,即
=a+c,即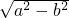 =c,
=c,
解得a2-b2=c2,即a2+c2=b2,故此三角形为直角三角形.
故选C.
点评:本题考查的是抛物线与x轴的交点及勾股定理的逆定理,解答此类题目时不要把抛物线上的点的坐标盲目代入求解,应按具体问题而定.
分析:抛物线y=x2-2ax+b2与x轴于M(a+c,0),把y=0代入抛物先的解析式,利用求根公式求出x的值即可求出a、b、c的关系式,进而可判断出三角形的形状.
解答:∵抛物线y=x2-2ax+b2交x轴于M(a+c,0),
∴当y=0时,x=a+c,
把y=0代入抛物线y=x2-2ax+b2交得,抛物线0=x2-2ax+b2,
解得,x=
 =a±
=a±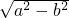 ,
,∵a、b、c是△ABC中∠A、∠B、∠C的对边,
∴a>0,b>0,c>0,
∴a+
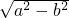 =a+c,即
=a+c,即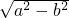 =c,
=c,解得a2-b2=c2,即a2+c2=b2,故此三角形为直角三角形.
故选C.
点评:本题考查的是抛物线与x轴的交点及勾股定理的逆定理,解答此类题目时不要把抛物线上的点的坐标盲目代入求解,应按具体问题而定.

练习册系列答案
相关题目
下列说法中正确的是( )
A、若AP=
| ||
| B、若AB=2PB,则P是AB的中点 | ||
| C、若AP=PB,则P是AB的中点 | ||
D、若AP=PB=
|
 行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.