题目内容
问题背景:
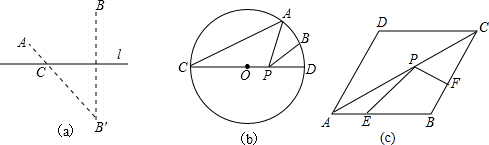
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接AB′与直线l交于点C,则点C即为所求.
实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B为弧AD的中点,P为直径CD上一动点,求:PA+PB的最小值,并写出解答过程.
知识拓展:
如图(c),在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是 .(直接写出答案)
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接AB′与直线l交于点C,则点C即为所求.

实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B为弧AD的中点,P为直径CD上一动点,求:PA+PB的最小值,并写出解答过程.
知识拓展:
如图(c),在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是
考点:圆的综合题,轴对称-最短路线问题
专题:
分析:(b)过点B作CD的垂线交CD于E点,交圆O于B1点,连接AB1,当P点为AB1与CD的交点时,AP+BP的值最小,根据勾股定理求出AB1,即可得出PA+PB的最小值;
(c)当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,易求E″F(F′)的长为
.
(c)当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,易求E″F(F′)的长为
| 5 |
解答: 实践运用:
实践运用:
(b)如图b,过点B作CD的垂线交CD于E点,交圆O于B1点,连接AB1,
当P点为AB1与CD的交点时,AP+BP的值最小.
过A点作CD的垂线交CD于F点,交圆O于H点,过B1作AH的垂线交AH于G点.
由垂径定理可知:BP=B1P;
∵∠ACD=30°,B为弧AD的中点,
∴OE=
,OF=1.
∴EF=B1G=
-1,又由于AG=AF+FG=
+1,
AB12=AG2+B1G2=(
+1)2+(
-1)2=8.
∴AB1=2
,即AP+BP的最小值为2
.

知识拓展:
(c)如图c所示,当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,PE+PF有最小值.
过点B作BM⊥AD于点M,
由题意可得:∠BF′E″=∠F′E″M=∠E″MB=90°,
∴四边形BME″F′为矩形,
则BM=E″F′,
在Rt△ABM中,AB=10,∠BAD=60°,
∴E″F=BM=AB•sin∠BAD=5
.
故答案为:5
.
 实践运用:
实践运用:(b)如图b,过点B作CD的垂线交CD于E点,交圆O于B1点,连接AB1,
当P点为AB1与CD的交点时,AP+BP的值最小.
过A点作CD的垂线交CD于F点,交圆O于H点,过B1作AH的垂线交AH于G点.
由垂径定理可知:BP=B1P;
∵∠ACD=30°,B为弧AD的中点,
∴OE=
| 3 |
∴EF=B1G=
| 3 |
| 3 |
AB12=AG2+B1G2=(
| 3 |
| 3 |
∴AB1=2
| 2 |
| 2 |

知识拓展:
(c)如图c所示,当点E(E′)关于AC对称点E″与P、F(F′)三点共线且与AD垂直时,PE+PF有最小值.
过点B作BM⊥AD于点M,
由题意可得:∠BF′E″=∠F′E″M=∠E″MB=90°,
∴四边形BME″F′为矩形,
则BM=E″F′,
在Rt△ABM中,AB=10,∠BAD=60°,
∴E″F=BM=AB•sin∠BAD=5
| 3 |
故答案为:5
| 3 |
点评:本题考查了菱形的性质和轴对称-最短路线问题,解题的关键是得到PE+PF的最小值为菱形ABCD中AD边的高.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
九年级1班共有49位同学,其中有25位男同学,班上每个同学的名字都各自写在一张小纸条上放入一个盒中搅匀.从中随便抽取一张纸条,那么下列说法正确的是( )
| A、抽到女同学的名字的概率大 |
| B、抽到男同学的名字的概率大 |
| C、抽到女同学的名字和男同学名字的概率一样大 |
| D、无法确定哪个概率大 |
为了考察两种小麦长势情况,从甲、乙两种小麦中分别抽取5株前,测得苗高(单位:厘米)如下:甲:6,8,9,9,9;乙:10,7,7,7,9.则甲、乙两种小麦的长势整齐程度是( )
| A、甲比乙整齐 |
| B、乙比甲整齐 |
| C、甲、乙整齐程度一样 |
| D、无法比较 |
若式子y=
在实数范围内有意义,则x的取值范围是( )
| ||
| 2-x |
| A、x≤3且x≠2 | B、x>3 |
| C、x≥3 | D、2≤x≤3 |
 已知,如图在△ABC中,AC=BC,AC⊥BC,直线EF交AC于F,交AB于E,交BC的延长线于D,且CF=CD,连接AD、BF,则AD与BF之间有何关系?请证明你的结论.
已知,如图在△ABC中,AC=BC,AC⊥BC,直线EF交AC于F,交AB于E,交BC的延长线于D,且CF=CD,连接AD、BF,则AD与BF之间有何关系?请证明你的结论.
 如图,已知∠AOB=50°,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB=
如图,已知∠AOB=50°,OM平分∠AOB,MA⊥OA于A,MB⊥OB于B,则∠MAB=