题目内容
如图扇形OAB,∠AOB=90°,⊙P与OA、OB分别相切于点F、E,并且与弧AB切于点C,若⊙P的半径为1,则扇形OAB的半径长为 .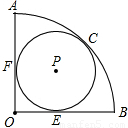
【答案】分析:连接PF、PE、OC,根据相切两圆的性质得出OC过P,根据切线的性质和正方形的判定推出四边形PFOE是正方形,推出PF=PE=OF=OE=1,由勾股定理求出OP,即可求出OC.
解答:解:
连接PF、PE、OC,
根据相切两圆的性质得出OC过P,
则OC=OA=OB,
∵⊙P切OA于F,切OB于E,
∴∠PEO=∠PFO=90°=∠AOB,
∴四边形PFOE是矩形,
∵PF=PE,
∴矩形PFOE是正方形,
∴PF=PE=OF=OE=1,
由勾股定理得:OP= =
= ,
,
∴OA=OC=OP+PC= +1,
+1,
故答案为: +1.
+1.
点评:本题考查了正方形的性质和判定,相切两圆的性质,勾股定理等知识点,关键是得出四边形PFOE是正方形,题目比较典型,是一道比较好的题目.
解答:解:

连接PF、PE、OC,
根据相切两圆的性质得出OC过P,
则OC=OA=OB,
∵⊙P切OA于F,切OB于E,
∴∠PEO=∠PFO=90°=∠AOB,
∴四边形PFOE是矩形,
∵PF=PE,
∴矩形PFOE是正方形,
∴PF=PE=OF=OE=1,
由勾股定理得:OP=
 =
= ,
,∴OA=OC=OP+PC=
 +1,
+1,故答案为:
 +1.
+1.点评:本题考查了正方形的性质和判定,相切两圆的性质,勾股定理等知识点,关键是得出四边形PFOE是正方形,题目比较典型,是一道比较好的题目.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
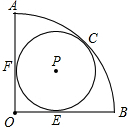 如图扇形OAB,∠AOB=90°,⊙P与OA、OB分别相切于点F、E,并且与弧AB切于点C,若⊙P的半径为1,则扇形OAB的半径长为
如图扇形OAB,∠AOB=90°,⊙P与OA、OB分别相切于点F、E,并且与弧AB切于点C,若⊙P的半径为1,则扇形OAB的半径长为