题目内容
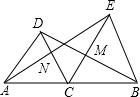 如图,点C在线段AB上,△ADC和△CEB都是等边三角形,连接AE交DC于N,连接BD交EC于M.则△MCB可看作是由△NCE经过旋转而得到的.请回答下列问题:
如图,点C在线段AB上,△ADC和△CEB都是等边三角形,连接AE交DC于N,连接BD交EC于M.则△MCB可看作是由△NCE经过旋转而得到的.请回答下列问题:
(1)旋转中心点是______;
(2)旋转角的度数是______;
(3)连接MN,则△MNC是什么三角形______;
(4)△DCB和△ACE是否全等,为什么?
解:(1)∵△MCB与△NCE的公共点为C点,
∴旋转中心点是C;
(2)∵△ADC和△CEB都是等边三角形,
∴∠DCE=60°,
∵图形旋转后MC与NC重合,
∴旋转角的度数是60°;
(3)∵△MCB可看作是由△NCE经过旋转而得到的,
∴△MCB≌△NCE,
∴NC=MC,
∵∠DCE=60°,
∴△MNC是等边三角形;
(4)∵△ACD与△BCE均是等边三角形,
∴AC=CD,BC=CE,∠ACD=BCE=60°,
∴∠ACE=∠DCB=120°,
∴△DCB≌△ACE.
分析:(1)找出△MCB与△NCE的公共点即为旋转中心点;
(2)找出旋转前后两三角形的对应边所夹的度数即为旋转角的度数;
(3)根据图形旋转的性质可得出CN=CM,再根据∠DCE=60°可知△MNC是等边三角形;
(4)根据图形旋转的性质可得出DC=AC,BC=CE,再根据,△ADC和△CEB都是等边三角形即可得出∠ACE=∠DCB,进而可得出结论.
点评:本题考查的是全等图形旋转的性质及全等三角形的判定定理,等边三角形的性质,熟知以上知识是解答此题的关键.
∴旋转中心点是C;
(2)∵△ADC和△CEB都是等边三角形,
∴∠DCE=60°,
∵图形旋转后MC与NC重合,
∴旋转角的度数是60°;
(3)∵△MCB可看作是由△NCE经过旋转而得到的,
∴△MCB≌△NCE,
∴NC=MC,
∵∠DCE=60°,
∴△MNC是等边三角形;
(4)∵△ACD与△BCE均是等边三角形,
∴AC=CD,BC=CE,∠ACD=BCE=60°,
∴∠ACE=∠DCB=120°,
∴△DCB≌△ACE.
分析:(1)找出△MCB与△NCE的公共点即为旋转中心点;
(2)找出旋转前后两三角形的对应边所夹的度数即为旋转角的度数;
(3)根据图形旋转的性质可得出CN=CM,再根据∠DCE=60°可知△MNC是等边三角形;
(4)根据图形旋转的性质可得出DC=AC,BC=CE,再根据,△ADC和△CEB都是等边三角形即可得出∠ACE=∠DCB,进而可得出结论.
点评:本题考查的是全等图形旋转的性质及全等三角形的判定定理,等边三角形的性质,熟知以上知识是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

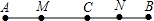
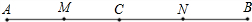
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长; 如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=
如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=