题目内容
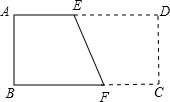 如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=
如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=分析:本题可利用相似解决,由于折叠,可知BD⊥EF,利用直角三角形相似的性质:对应边成比例求得结果.
解答: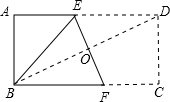 解:链接BD,如下图所示:
解:链接BD,如下图所示:
∵折叠,使点D与点B重合,
∴BD⊥EF,BO=DO,
∵矩形ABCD,
∴∠C=90°,BD=
=
=3
cm,BO=
cm
易知:△BOF∽△BCD,
∴
=
,即
=
,
∴OF=
cm,
∴EF=
cm.
故答案为:
.
 解:链接BD,如下图所示:
解:链接BD,如下图所示:∵折叠,使点D与点B重合,
∴BD⊥EF,BO=DO,
∵矩形ABCD,
∴∠C=90°,BD=
| BC2+CD 2 |
| 92+32 |
| 10 |
3
| ||
| 2 |
易知:△BOF∽△BCD,
∴
| BO |
| BC |
| OF |
| CD |
| ||||
| 9 |
| OF |
| 3 |
∴OF=
| ||
| 2 |
∴EF=
| 10 |
故答案为:
| 10 |
点评:本题考查的是图形翻折变换的性质,注意掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解答此类题目首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.

练习册系列答案
相关题目
 48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M.
48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M. 8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )
8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )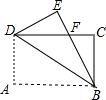 如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为
如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为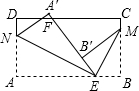 如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互