题目内容
【题目】如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，当P运动到B点时，P、Q两点同时停止运动．设P点运动的时间为t，△APQ的面积为S，则S与t的函数关系的图象是（ ）
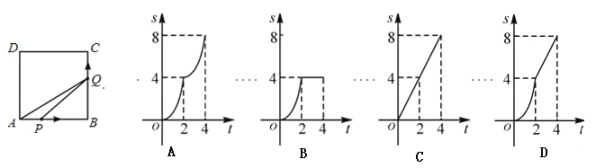
【答案】D．
【解析】
试题解析：①点P在AB上运动，点Q在BC上运动，此时AP=t，QB=2t，
故可得S=
APQB=t2，函数图象为抛物线；
②点P在AB上运动，点Q在CD上运动，
此时AP=t，△APQ底边AP上的高保持不变，为正方形的边长4，
故可得S=AP×4=2t，函数图象为一次函数．
综上可得总过程的函数图象，先是抛物线，然后是一次增函数．
故选D．
练习册系列答案
相关题目
