题目内容
四边形ABCD为菱形，E为BC边上的中点，P为对角线BD上一点，要使PE+PC最小，则应满足
- A.PE=PC
- B.PE⊥PC
- C.PB=PD
- D.∠BAE=∠BCP
D
分析：当PE+PC=PE+AP=AE，取最小值，所以要证明△ABP≌△CBP，即满足的条件是∠BAE=∠BCP．
解答：连接AC，AE，AE与BD交于点P，
此时，PE+PC=PE+AP=AE，取最小值，
应满足的条件是∠BAE=∠BCP，
可证明△ABP≌△CBP，
PA=PC．
故选D．
点评：考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用．
分析：当PE+PC=PE+AP=AE，取最小值，所以要证明△ABP≌△CBP，即满足的条件是∠BAE=∠BCP．
解答：连接AC，AE，AE与BD交于点P，
此时，PE+PC=PE+AP=AE，取最小值，
应满足的条件是∠BAE=∠BCP，
可证明△ABP≌△CBP，
PA=PC．
故选D．
点评：考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
意一点，过点P作PC⊥x轴于点C，PO⊥y轴于点D．
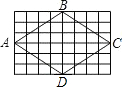如图，四边形ABCD为菱形，则tan| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
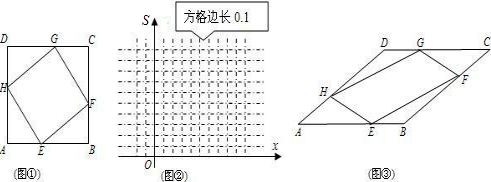
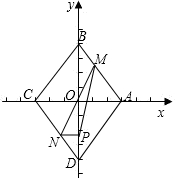点N，过点N作NP⊥BD，交BD于点P，连接MP，当动点M运动了t秒时．
如图，每个小方格都是边长为1个单位的小正方形，B，C，D三点都是格点（每个小方格的顶点叫格点）．