题目内容

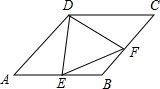精英家教网In the figure1，ABCD is a diamond，points E and F lie on its sides AB and BC respectively，such that
AE
BE
=
BF
CF
，and△DEFis a regular triangle． Then∠BADis equal to （　　）（英汉小词典：diamond菱形；regular triangle正三角形）
A、40°B、60°
C、80°D、100°
分析：根据菱形ABCD中，
AE
BE
=
BF
FC
，和AB=BC，等边△DEF，利用余弦定理可以求出，即可得∠BAD的值．
解答：精英家教网解：设菱形ABCD边长为x，AE=a，等边△DEF边长为y，
∵
AE
BE
=
BF
FC
，AB=BC，
∴AE=FB，BE=CF，
∴AE=BF=a，BE=CF=x-a，
∵△DEF是正三角形，
∠A=∠C，∠B=180°-∠A，
cosA=cos（180-B）=-cosB，
EF2=BE2+FB2-2BE•FBcosB，
=（x-a）2+a2-2（x-a）a•cosB，①
DE2=AD2+AE2-2AD•AEcosA，
=x2+（x-a）2-2x（x-a）cosA，②
②-①得：
x2-a2-2（x-a）cosA（x+a），
∴x2-a2=2（x-a）cosA（x+a），
∴2cosA=1，
∴cosA=
1
2
，
∴∠BAD=60°，
故选 B．
点评：本题考查了全等三角形的证明，考查了等边三角形各边长相等、各内角为60°的性质，考查了菱形各边长相等的性质，利用余弦定理得出是解题的关键．
练习册系列答案
相关题目
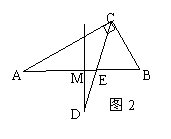
16、In Fig．，In the Rt△ABC，∠ACB=90°，∠A=30°，CD is the bisector to∠ACB，MD is the perpendicular to BA and MD through the midpoint of segment AB，then∠CDM=
15°
．
（英语小词典：bisector：平分线；perpendicular：垂线；midpoint：中点）
In right Fig，if the length of the segment AB is 1，M is the midpoint  of the segment AB，and point C divides the segment MB into two partssuch that MC：CB=1：2，then the length of AC is
 
．
（英汉词典：length长度；segment线段；midpoint中点；divides…into分为，分成）

In right Fig.，if the length of the segment AB is 1，M is the midpoint

            of the segment AB，and point C divides the segment MB into two parts

            such that MC：CB=1：2，then the length of AC is       。

   (英汉词典：length 长度；segment 线段；midpoint 中点；divides…into 分为，分成)

 

 
In right Fig，if the length of the segment AB is 1，M is the midpoint  of the segment AB，and point C divides the segment MB into two partssuch that MC：CB=1：2，then the length of AC is______．
（英汉词典：length长度；segment线段；midpoint中点；divides…into分为，分成）

In Fig.2,In the Rt△ABC，∠ACB=900，∠A=300，CD is the bisector to

∠ACB，MD is the perpendicular to BA and MD through the midpoint of segment AB，thrn ∠CDM=         .(英语小词典：bisector：平分线；perpendicular：垂线；midpoint：中点)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网