题目内容
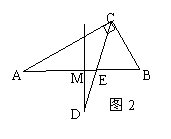
 16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=
16、In Fig.,In the Rt△ABC,∠ACB=90°,∠A=30°,CD is the bisector to∠ACB,MD is the perpendicular to BA and MD through the midpoint of segment AB,then∠CDM=15°
.(英语小词典:bisector:平分线;perpendicular:垂线;midpoint:中点)
分析:连接CM,根据直角三角形斜边上的中线等于斜边的一半可得到CM=AM,再根据角平分线的性质可求得∠MCE的度数,由三角形的外角的性质及三角形的内角和定理不难求得∠CDM的度数.
解答: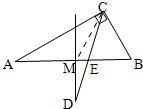 解:连接CM.
解:连接CM.
∵点M是斜边AB上的中点,∠A=30°,
∴CM=AM,
∴∠A=∠ACM=30°,
∵CD是∠ACB的角平分线,
∴∠ACE=45°,
∴∠MCE=45°-30°=15°,
∵∠CME=∠A+∠ACM=2∠A=60°,MD⊥AB,
∴∠CMD=60°+90°=150°,
∵∠MCE+∠CMD+∠CDM=180°,
∴∠CDM=15°.
故答案为:15°.
 解:连接CM.
解:连接CM.∵点M是斜边AB上的中点,∠A=30°,
∴CM=AM,
∴∠A=∠ACM=30°,
∵CD是∠ACB的角平分线,
∴∠ACE=45°,
∴∠MCE=45°-30°=15°,
∵∠CME=∠A+∠ACM=2∠A=60°,MD⊥AB,
∴∠CMD=60°+90°=150°,
∵∠MCE+∠CMD+∠CDM=180°,
∴∠CDM=15°.
故答案为:15°.
点评:此题主要考查学生对直角三角形斜边上的中线的性质,三角形的外角的性质及三角形内角和定理的综合运用能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
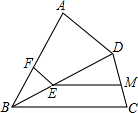 In fig 1,ABCD is a quadrilsteral,E is a point the diagonal BD,EF∥AD,EM∥BC,then the value of
In fig 1,ABCD is a quadrilsteral,E is a point the diagonal BD,EF∥AD,EM∥BC,then the value of | EF |
| DA |
| EM |
| BC |
(英汉词典:fig figure的缩写,图;quadrilateral四边形;diagonal对角线;value数值;variable变量;to depend on取决于;position位置)
四边形ABCD中,E是对角线BD上一点,EF∥AD,EM∥BC,则
| EF |
| DA |
| EM |
| BC |
| A、greater than 1(大于1) |
| B、equal to 1(等于1) |
| C、less than 1(小于1) |
| D、variable depending on the position of E(不能确定,与E的位置有关) |
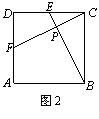
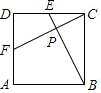 Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is
Suppose that in Fig.2,the length of side of square ABCD is 1,E and F are mid-points of CD and AD respectively,GE and CF intersect at a point P.Then the length of line segment CP is