题目内容
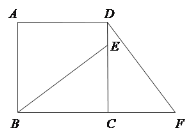
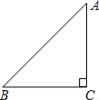
【题目】在RtABC中,∠C=90°,AC=BC=![]() (如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.
(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.
【答案】![]()
【解析】
连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解.
解:如图,连接BB′,
∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,
∴AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴AB=BB′,
在△ABC′和△B′BC′中,
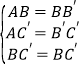 ,
,
∴△ABC′≌△B′BC′(SSS),
∴∠ABC′=∠B′BC′,
延长BC′交AB′于D,
则BD⊥AB′,
∵∠C=90°,AC=BC=![]() ,
,
∴AB=2,
∴BD=2×![]() =
=![]() ,
,
C′D=![]() ×2=1,
×2=1,
∴BC′=BD﹣C′D=![]() ﹣1.
﹣1.

故答案是:![]() ﹣1.
﹣1.

练习册系列答案
相关题目