题目内容
先阅读,再填空解答:方程x2-3x-4=0的根是:x1=-1,x2=4,则x1+x2=3,x1x2=-4;
方程3x2+10x+8=0的根是:x1=-2,x2=-
| 4 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
(1)方程2x2+x-3=0的根是:x1=
(2)若x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0,且a,b,c为常数)的两个实数根,那么x1+x2,x1x2与系数a,b,c的关系是:x1+x2=
(3)如果x1,x2是方程x2+x-3=0的两个根,根据(2)所得结论,求x12+x22的值.
分析:(1)解方程求出方程的两个根,再利用根与系数的关系求出两根之和,与两根之积;
(2)根据根与系数的关系可知x1+x2=-
,x1x2=
;
(3)利用完全平方公式把x12+x22变化成(x1+x2)2-2x1x2的形式,再利用根与系数的关系求值.
(2)根据根与系数的关系可知x1+x2=-
| b |
| a |
| c |
| a |
(3)利用完全平方公式把x12+x22变化成(x1+x2)2-2x1x2的形式,再利用根与系数的关系求值.
解答:解:(1)∵2x2+x-3=0,
∴(2x+3)(x-1)=0,
∴x1=-
,x2=1,
∴x1+x2=-
,x1x2=-
;
故填空答案:-
,1,-
,-
.
(2)x1+x2=-
,x1x2=
;
故填空答案:-
,
.
(3)解:根据(2)可知:
x1+x2=-1,x1x2=-3,
则x12+x22=(x1+x2)2-2x1x2
=(-1)2-2×(-3)
=7.
∴(2x+3)(x-1)=0,
∴x1=-
| 3 |
| 2 |
∴x1+x2=-
| 1 |
| 2 |
| 3 |
| 2 |
故填空答案:-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)x1+x2=-
| b |
| a |
| c |
| a |
故填空答案:-
| b |
| a |
| c |
| a |
(3)解:根据(2)可知:
x1+x2=-1,x1x2=-3,
则x12+x22=(x1+x2)2-2x1x2
=(-1)2-2×(-3)
=7.
点评:本题是一个信息题,通过阅读题目所给材料,然后根据材料解决题目问题,注意题目中每个小题的联系,在解题的过程中善于发现规律是解决本题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
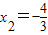 ,则x1+x2=-
,则x1+x2=-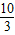 ,x1x2=
,x1x2= .
. ,则x1+x2=-
,则x1+x2=- ,x1x2=
,x1x2= .
.