题目内容
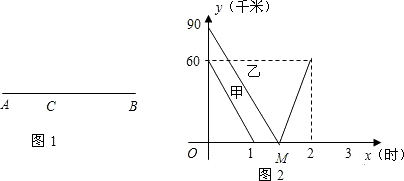
如图①,一条笔直的公路上有A、B、C三地,B、C两地相距 150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A 地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.

根据图象进行以下探究:
(1)请在图①中标出 A地的位置,并作简要说明;
(2)甲的速度为
(3)求图②中M点的坐标,并解释该点的实际意义;
(4)在图②中补全甲车到达C地的函数图象,求甲车到A地的距离y1与行驶时间x的函数关系式;
(5)出发多长时间,甲、乙两车距A点的距离相等?

根据图象进行以下探究:
(1)请在图①中标出 A地的位置,并作简要说明;
(2)甲的速度为
60
60
km/h,乙的速度为75
75
km/h;(3)求图②中M点的坐标,并解释该点的实际意义;
(4)在图②中补全甲车到达C地的函数图象,求甲车到A地的距离y1与行驶时间x的函数关系式;
(5)出发多长时间,甲、乙两车距A点的距离相等?
分析:(1)由题意结合函数图象可以得出点A的位置;
(2)由速度=路程÷时间就可以得出甲、乙的速度;
(3)由路程÷乙的速度就可以得出M的横坐标从而求出M的坐标,由条件就可以得出M点的意义;
(4)由路程求出甲车到达C地的时间就可以画出甲车到达C地的函数图象,由待定系数法就可以求出y1与行驶时间x的函数关系式;
(5)设出发x小时时,甲、乙两车距A点的距离相等,由路程之间的数量关系建立方程求出其解即可.
(2)由速度=路程÷时间就可以得出甲、乙的速度;
(3)由路程÷乙的速度就可以得出M的横坐标从而求出M的坐标,由条件就可以得出M点的意义;
(4)由路程求出甲车到达C地的时间就可以画出甲车到达C地的函数图象,由待定系数法就可以求出y1与行驶时间x的函数关系式;
(5)设出发x小时时,甲、乙两车距A点的距离相等,由路程之间的数量关系建立方程求出其解即可.
解答:解:(1)由函数图象可以得出A点在线段BC上距B点60km的地方,即AB=60km或者AC=90km,如图①:
(2)由题意,得
60÷1=60,150÷2=75,
故答案为:60,75;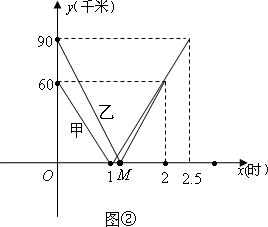
(3)由图象,得
90÷75=
∴M(
,0),乙车到达A地的时间为
小时;
(4)由图象,得
150÷60=2.5,
∴补全图象为如图②:
设y1与行驶时间x的函数关系式为y1=kx+b,由题意,得
或
,
解得:
或
∴y1=
;
(5)设出发x小时时,甲、乙两车距A点的距离相等,由题意,得
60-60x=90-75x或60x+75x=60+90,
解得:x1=
,x2=2.
答:出发
小时或2小时时,甲、乙两车距A点的距离相等.

(2)由题意,得
60÷1=60,150÷2=75,
故答案为:60,75;

(3)由图象,得
90÷75=
| 6 |
| 5 |
∴M(
| 6 |
| 5 |
| 6 |
| 5 |
(4)由图象,得
150÷60=2.5,
∴补全图象为如图②:
设y1与行驶时间x的函数关系式为y1=kx+b,由题意,得
|
|
解得:
|
|
∴y1=
|
(5)设出发x小时时,甲、乙两车距A点的距离相等,由题意,得
60-60x=90-75x或60x+75x=60+90,
解得:x1=
| 10 |
| 9 |
答:出发
| 10 |
| 9 |
点评:本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,列一元一次方程解实际问题的运用,解答时分析求出函数图象的意义是关键.

练习册系列答案
相关题目
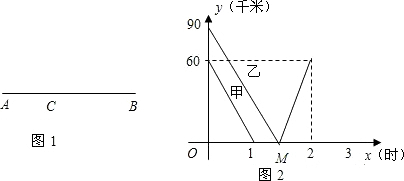
 (2013•南宁)在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
(2013•南宁)在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题: