题目内容
在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度(0<α≤180°)得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于P、Q.
(1)四边形OABC的形状是 ,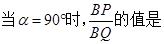 ;
;
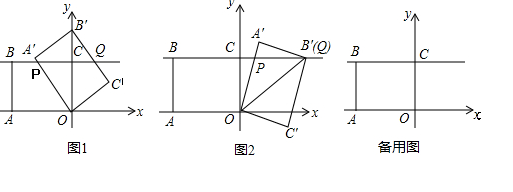
(2)①如图1,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求PQ的长;
②如图2,当四边形OA′B′C′的顶点B′落在直线BC上时,求PQ的长.
(3)小明在旋转中发现,当点P位于点B的右侧时,总存在线段PQ与线段 相等;同时存在着特殊情况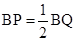 ,求出此时P点的坐标。
,求出此时P点的坐标。

(1)四边形OABC的形状是 ,
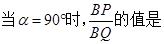 ;
;(2)①如图1,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求PQ的长;
②如图2,当四边形OA′B′C′的顶点B′落在直线BC上时,求PQ的长.
(3)小明在旋转中发现,当点P位于点B的右侧时,总存在线段PQ与线段 相等;同时存在着特殊情况
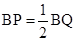 ,求出此时P点的坐标。
,求出此时P点的坐标。解:(1)矩形  (2)①PQ=7.5 6分
(2)①PQ=7.5 6分
② (3)OP
(3)OP 
 (2)①PQ=7.5 6分
(2)①PQ=7.5 6分②
 (3)OP
(3)OP 
试题分析:解:(1)∵O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),
∴OA=BC=8,OC=AB=6,∠AOA′=90°,
∴四边形OABC的形状是矩形;
当α=90°时,P与C重合,如右图,
根据题意,得BP/PQ=4/3,
则BP/BQ=4/7
(2)①如图1,∵∠POC=∠B'OA',∠PCO=∠OA'B'=90°,
∴△COP∽△A'OB',
∴CP/A1B=OC/OA1
,即CP/6=6/8
∴CP=4.5
同理△B'CQ∽△B'C'O,CQ/OC=B1C/B1C,即
∴CQ=3,
PQ=CP+CQ=7.5
②如图2,∵在△OCP和△B'A'P中,
△OCP≌△B'A'P(AAS),
∴OP=B'P,即OP=PQ,
设PQ=x.
在Rt△OCP中,(8-x)2+62=x2,
解得x=25/4
故所求PQ的长为25/4;
(3)当点P位于点B的右侧时,总存在线段PQ与线段OP相等;同时存在着特殊情况BP=1/2BQ,此时点P的坐标是P(7/4,6).理由如下:
如备用图,过点Q画QH⊥OA′于H,连接OQ,则QH=OC′=OC,∵S△POQ=1/2PQ•OC,S△POQ=1/2OP•QH,
∴PQ=OP.
设BP=x,
∵BP=1/2BQ,
∴BQ=2x,
∵点P在点B右侧,
∴OP=PQ=BQ-BP=x,PC=8-x.
在Rt△PCO中,(8-x)2+62=x2,
解得x=25/4.
点评:本题考查了旋转的性质,矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理.特别注意在旋转的过程中的对应线段相等,能够用一个未知数表示同一个直角三角形的未知边,根据勾股定理列方程求解.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目








 、
、 为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为
为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为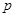 ,如果在点
,如果在点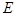 的运动过程中,
的运动过程中,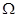 四边形”, 此时
四边形”, 此时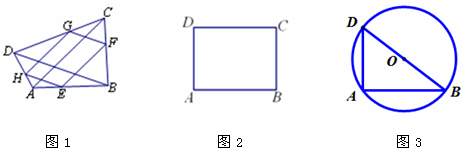
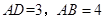 ,点
,点 为
为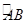 上的一动点,将△
上的一动点,将△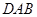 沿
沿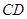 的中垂线翻折,得到△
的中垂线翻折,得到△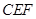 .当点
.当点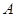 、
、 、
、 、
、 、
、 中的任意四个点为顶点的“
中的任意四个点为顶点的“