题目内容
【题目】如图,一艘轮船以每小时40海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上.当轮船到达灯塔C的正东方向D处时,又航行了多少海里?
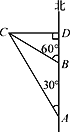
【答案】当轮船到达灯塔C的正东方向D处时,又航行了40海里.
【解析】试题分析:因为∠CBD是△ABC的外角,所以∠BCA=∠CBD-∠A=60°-30°=30°,所以BC =AB=2×40=80(海里),在Rt△BDC中, ∠CBD=60°,所以∠BCD=30°,所以BD= ![]() =40(海里).
=40(海里).
试题解析:∵CD⊥DB,∠CBD=60°,
∴∠DCB=30°,
∴DB=![]() BC,
BC,
∴BC=2DB,
又∵∠BCA=60°-30°=30°,
∴BC=BA,
∴BC=2×40=80(海里),
∴DB=40海里,
答:当轮船到达灯塔C的正东方向D处时,又航行了40海里.

练习册系列答案
相关题目
【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣15.5 | ﹣5 | ﹣3.5 | ﹣2 | ﹣3.5 | … |
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .