题目内容
 (2012•安庆二模)如图是某小区的两座高楼,小明乘坐观光电梯在C处测得另一大楼顶部A的仰角为37°,电梯下降10m到D处时,又测得其底部B的俯角为48°.已知两座楼都为30层,每层高约2.8m,请帮小明求出两座高楼间的距离(参考数据:sin37°≈
(2012•安庆二模)如图是某小区的两座高楼,小明乘坐观光电梯在C处测得另一大楼顶部A的仰角为37°,电梯下降10m到D处时,又测得其底部B的俯角为48°.已知两座楼都为30层,每层高约2.8m,请帮小明求出两座高楼间的距离(参考数据:sin37°≈| 3 |
| 5 |
| 3 |
| 4 |
| 7 |
| 10 |
| 11 |
| 10 |
分析:先设两座高楼间的距离为x,在Rt△ACE中,由锐角三角函数的定义可知,AE=CEtan37°,即AE=x•tan37°;同理在Rt△DBF中,BF=x•tan48°,再由AE+BF+EF=30×2.8,EF=10即可得出AE+BF的值,进而得出结论.
解答:解:设两座高楼间的距离为x,
在Rt△ACE中,
AE=CEtan37°,即AE=x•tan37°;
同理在Rt△DBF中,
BF=x•tan48°,
∵AE+BF+EF=30×2.8,EF=10
∴AE+BF=74,即x•tan37°+x•tan48°=74,即x(
+
)=74,
解得x=40米.
答:两座高楼间的距离为40米.
在Rt△ACE中,
AE=CEtan37°,即AE=x•tan37°;
同理在Rt△DBF中,
BF=x•tan48°,
∵AE+BF+EF=30×2.8,EF=10
∴AE+BF=74,即x•tan37°+x•tan48°=74,即x(
| 3 |
| 4 |
| 11 |
| 10 |
解得x=40米.
答:两座高楼间的距离为40米.
点评:本题考查的是解直角三角形的应用-仰角俯角问题,根据题意设出两层楼之间的距离,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
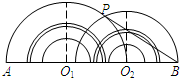 (2012•安庆二模)如图,大小两个量角器的零度线都在直线AB上,而且小量角器的中心在大量角器的外边缘上.如果它们外边缘上的公共点P在大量角器上对应的度数为50°,那么∠PBA为的度数( )
(2012•安庆二模)如图,大小两个量角器的零度线都在直线AB上,而且小量角器的中心在大量角器的外边缘上.如果它们外边缘上的公共点P在大量角器上对应的度数为50°,那么∠PBA为的度数( )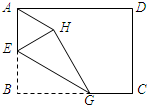 (2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( )
(2012•安庆二模)如图,已知矩形纸片ABCD,E是AB边的中点,点G为BC边上的一点,现沿EG将纸片折叠,使点B落在纸片上的点H处,连接AH.若AB=EG,则与∠BEG相等的角的个数为( ) (2012•安庆二模)如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q、与y轴相交于点M(0,4)和N(0,16),则点P的坐标是
(2012•安庆二模)如图,在平面直角坐标系中,点P在第一象限,⊙P与x轴相切于点Q、与y轴相交于点M(0,4)和N(0,16),则点P的坐标是