题目内容
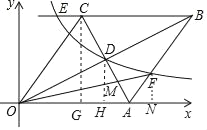
【题目】如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6
(x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6![]() ;④S△AFM:S△AOM=1:3.其中正确的结论是( )
;④S△AFM:S△AOM=1:3.其中正确的结论是( )

A. ①②B. ①③C. ①②③D. ①②③④
【答案】D
【解析】
首先过点D作DH⊥x轴于点H,由菱形OABC中,ACOB=40,可求得菱形OABC的面积,继而求得△AOD的面积,则可求得高DH,然后由射影定理,可得DH2=OHAH,继而求得①正确;过C作CG⊥x轴于点G,根据平行线等分线段定理和三角形的中位线的性质得到CG=2DH=4,AG=2AH=2,求得C(3,4),E(2,4),于是得到CE=1,故②正确;根据勾股定理得到AC+OB=6![]() ;故③正确;过F作FN⊥x轴于点N,设FN=4x,AN=3x,根据三角形的面积公式得到x=
;故③正确;过F作FN⊥x轴于点N,设FN=4x,AN=3x,根据三角形的面积公式得到x=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,于是得到S△AFM:S△AOM=1:3,故④正确.
,于是得到S△AFM:S△AOM=1:3,故④正确.
解:过点D作DH⊥x轴于点H,
∵菱形OABC中,ACOB=40,
∴S菱形OABC=![]() ACOB=20,
ACOB=20,
∴S△OAD=![]() S菱形OABC=5,
S菱形OABC=5,
∵S△OAD=![]() OADH,且OA=5,
OADH,且OA=5,
∴DH=2,
∵DH2=OHAH=4,OH+AH=5,
∴OH=4,AH=1,
∴点D(4,2),
∴k=4×2=8.故①正确;
过C作CG⊥x轴于点G,
∴DH∥CG,
∵AD=CD,
∴CG=2DH=4,AG=2AH=2,
∴OG=3,
∴C(3,4),
∴E(2,4),
∴CE=1,故②正确;
∵CG=4,AG=2,
∴AC=![]() =2
=2![]() ,
,
∵DH=2,OH=4,
∴OD=2![]() ,
,
∴OB=4![]() ,
,
∴AC+OB=6![]() ;故③正确;
;故③正确;
过F作FN⊥x轴于点N,
∵OC∥AB,
∴∠COG=∠FAN,
∴tan∠COG=tan∠FAN=![]() =
=![]() =
=![]() ,
,
设FN=4x,AN=3x,
∴S△OFN=![]() (5+3x)×4x=4,
(5+3x)×4x=4,
∴x=![]() ,
,
∴FN=![]() ,AN=1,
,AN=1,
∵△OCG∽△AFN,
∴![]() =3,
=3,
∵OC∥AF,
∴△AMF∽△CMO,
∴![]() =3,
=3,
∴S△AFM:S△AOM=1:3,故④正确,
故选:D.