题目内容
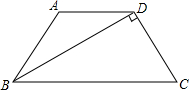
已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.
(1)求证:△MED为等腰三角形;
(2)求证:∠EMD=2∠DAC.
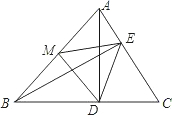
(1)求证:△MED为等腰三角形;
(2)求证:∠EMD=2∠DAC.

证明:(1)∵M为AB边的中点,AD⊥BC,BE⊥AC,
∴ME=
AB,MD=
AB,
∴ME=MD,
∴△MED为等腰三角形;
(2)∵ME=
AB=MA,
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=
AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC.
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MD,
∴△MED为等腰三角形;
(2)∵ME=
| 1 |
| 2 |
∴∠MAE=∠MEA,
∴∠BME=2∠MAE,
同理,MD=
| 1 |
| 2 |
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC.

练习册系列答案
相关题目