题目内容
【题目】如图，直线l1的函数表达式为y1=﹣3x+3，且l1与x轴交于点D，直线l2：y2=kx+b经过点A，B，与直线l1交于点C．
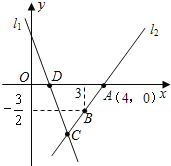
（1）求直线l2的函数表达式及C点坐标；
（2）求△ADC的面积；
（3）当x满足何值时，y1＞y2；（直接写出结果）
（4）在直角坐标系中有点E，和A，C，D构成平行四边形，请直接写出E点的坐标．
【答案】（1）直线l2的解析式为y2=
x﹣6；点C的坐标为（2，﹣3）；（2）
；（3）x＜2；（4）E1（5，﹣3）、E2（3，3）、E3（﹣1，﹣3）．
【解析】
试题分析：（1）利用待定系数法求出直线l2的解析式，利用二元一次方程组求出两条直线的交点C的坐标；
（2）根据坐标与图形图中求出点D的坐标，根据三角形的面积公式计算即可；
（3）运用数形结合思想解答；
（4）分以AC为对角线、以AD为对角线、以CD为对角线三种情况，根据平行四边形的性质解答即可．
解：（1）∵点A（4，0）、B（3，﹣）在直线l2：y2=kx+b上，
∴
，
解得：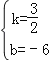
．
∴直线l2的解析式为y2=x﹣6；
由
，
解得
．
∴点C的坐标为（2，﹣3）；
（2）∵点D是直线l1：y=﹣3x+3与x轴的交点，
∴y=0时，0=﹣3x+3，解得x=1，
∴D（1，0），
∵A（4，0），
∴AD=4﹣1=3，
∴△ADC的面积=
×3×3=；
（3）由图象可知，当x＜2时，y1＞y2；
（4）符合条件的E点的坐标为E1（5，﹣3）、E2（3，3）、E3（﹣1，﹣3），
①以AC为对角线时，
∵四边形ADCE是平行四边形，
∴CE∥DA，CE=DA=3，
∴将点C（2，﹣3）向右平移3个单位得到点E，即E1（5，﹣3）；
②以AD为对角线时，
∵四边形ACDE是平行四边形，
∴CE与AD互相平分，即CE与AD的中点重合，则E2（3，3）；
③以CD为对角线时，
∵四边形ADEC是平行四边形，
∴CE∥AD，CE=AD=3，
∴将点C（2，﹣3）向左平移3个单位得到点E，即E3（﹣1，﹣3）；
综上所述，符合条件的E点的坐标为E1（5，﹣3）、E2（3，3）、E3（﹣1，﹣3）．
