题目内容
下列结论成立的是
- A.三条线段a,b,c,若满足a+b>c,则他们能组成一个三角形
- B.若a,b,c为常数,则y=ax2+bx+c是关于x的二次函数
- C.直角三角形的两边长是3,4,则它的第三边一定是5
- D.若等腰三角形的一个角是50°,则这个等腰三角形的顶角是50°或80°
D
分析:根据三角形的三边关系、二次函数的定义、勾股定理以及等腰三角形的性质逐项分析即可.
解答:A、三条线段a,b,c,若满足a+b>c,a-b<c,则他们能组成一个三角形,以上两个条件缺一不可,故该命题错误;
B、若a,b,c为常数,a≠0,则y=ax2+bx+c是关于x的二次函数,故该命题错误;
C、直角三角形的两边长是3,4,则它的第三边是5或4,故该命题错误;
D、等腰三角形的一个角是50°,则这个等腰三角形的顶角是50°或80°,故该命正确;
故选D.
点评:本题考查了三角形的三边关系、二次函数的定义、勾股定理以及等腰三角形的性质,解题的关键是正确掌握各种性质和定义.
分析:根据三角形的三边关系、二次函数的定义、勾股定理以及等腰三角形的性质逐项分析即可.
解答:A、三条线段a,b,c,若满足a+b>c,a-b<c,则他们能组成一个三角形,以上两个条件缺一不可,故该命题错误;
B、若a,b,c为常数,a≠0,则y=ax2+bx+c是关于x的二次函数,故该命题错误;
C、直角三角形的两边长是3,4,则它的第三边是5或4,故该命题错误;
D、等腰三角形的一个角是50°,则这个等腰三角形的顶角是50°或80°,故该命正确;
故选D.
点评:本题考查了三角形的三边关系、二次函数的定义、勾股定理以及等腰三角形的性质,解题的关键是正确掌握各种性质和定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )
A、sinA=
| ||
B、cosA=
| ||
C、tanA=
| ||
D、cotA=
|
在△ABC中,∠A,∠B,∠C对边分别为a,b,c,a=5,b=12,c=13,下列结论成立的是( )
A、sinA=
| ||
B、cosA=
| ||
C、tanA=
| ||
D、cosB=
|
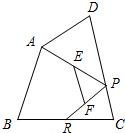 10、如图,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
10、如图,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( ) 如图所示,DE⊥AB,DF⊥AC,AE=AF,则下列结论成立的是( )
如图所示,DE⊥AB,DF⊥AC,AE=AF,则下列结论成立的是( )