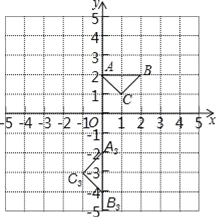
题目内容
【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.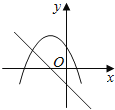 B.
B.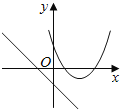 C.
C.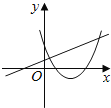 D.
D.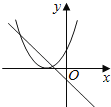
【答案】D
【解析】
试题分析:本题主要考查一次函数和二次函数的图象所经过的象限的问题,关键是m的正负的确定,对于二次函数y=ax2+bx+c,当a>0时,开口向上;当a<0时,开口向下.对称轴为x=![]() ,与y轴的交点坐标为(0,c).
,与y轴的交点坐标为(0,c).
解:解法一:逐项分析
A、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B、由函数y=mx+m的图象可知m<0,对称轴为x=![]() =
=![]() =
=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C、由函数y=mx+m的图象可知m>0,即函数y=﹣mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D、由函数y=mx+m的图象可知m<0,即函数y=﹣mx2+2x+2开口方向朝上,对称轴为x=![]() =
=![]() =
=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
解法二:系统分析
当二次函数开口向下时,﹣m<0,m>0,
一次函数图象过一、二、三象限.
当二次函数开口向上时,﹣m>0,m<0,
对称轴x=![]() <0,
<0,
这时二次函数图象的对称轴在y轴左侧,
一次函数图象过二、三、四象限.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目