题目内容
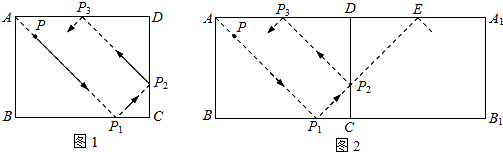
阅读材料:如图1所示,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系,连接OA,OB,OC。
∵S=S△OAB+S△OBC+S△OCA
又∵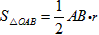 ,
,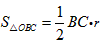 ,
,
∴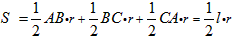
∴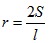
解决问题:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1,a2,a3,…,an,合理猜想其内切圆半径公式(不需说明理由)。
∵S=S△OAB+S△OBC+S△OCA
又∵
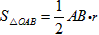 ,
,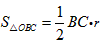 ,
,
∴
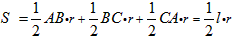
∴
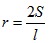
解决问题:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1,a2,a3,…,an,合理猜想其内切圆半径公式(不需说明理由)。
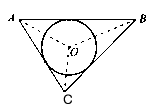

图1 图2
解:(1)∵ ,
,
∴三角形为直角三角形,
面积 ,
,
∴ ;
;
(2)设四边形ABCD内切圆的圆心为O,连结OA,OB,OC,OD,则

∴ ;
;
(3) 。
。
 ,
,∴三角形为直角三角形,
面积
 ,
,∴
 ;
;(2)设四边形ABCD内切圆的圆心为O,连结OA,OB,OC,OD,则


∴
 ;
;(3)
 。
。
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
| |||||||||||||||||||||||