题目内容
【题目】如图所示,在长方形ABCD中,AB=8,BC=4,将长方形沿AC折叠,使点D落在点D′处,求重叠部分△AFC的面积.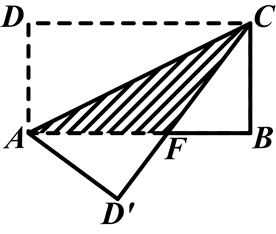
【答案】解:在长方形ABCD中,
∵AB∥CD,
∴∠BAC=∠DCA.
又由折叠的性质可得∠DCA=∠FCA.
∴∠BAC=∠FCA.
∴AF=CF.
设AF=x,则BF=AB-AF=8-x.
在Rt△BCF中,BC=4,BF=8-x,CF=x,
∴42+(8-x)2=x2 . 解得x=5.
∴ ![]() .
.
【解析】由矩形性质得到∠BAC=∠DCA;由折叠的性质得∠DCA=∠FCA;根据等量代换可得∠BAC=∠FCA;由等边对等角得AF=CF.设AF=x,则BF=AB-AF=8-x.在Rt△BCF中,由勾股定理得到一个一元二次方程,42+(8-x)2=x2 . 解得x=5.再由三角形面积公式即可求得。
【考点精析】本题主要考查了三角形的面积和勾股定理的概念的相关知识点,需要掌握三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目