题目内容
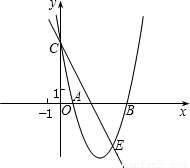
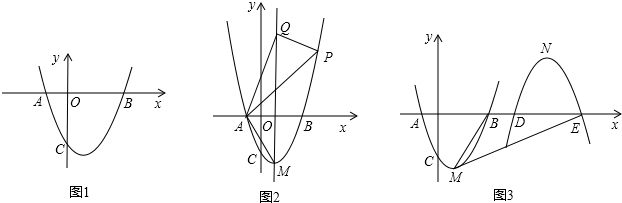
已知:如图1,二次函数y=a(x-1)2-4的图象交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,且OB=3OA.
(1)求二次函数的解析式;
(2)如图2,M是抛物线的顶点,P是抛物线在B点右侧上一点,Q是对称轴上一点,并且AQ⊥PQ,是否存在这样的点P,使得∠PAQ=∠AMQ?若存在,请求出P点坐标;若不存在,请说明理由.
(3)如图3,设(1)中抛物线的顶点为M,R为x轴正半轴上一点,将(1)中抛物线绕R旋转180°得到抛物线C1:y=-a (x-h)2+k交x轴于D,E两点.若tan∠BME=1,求R点的坐标.
解:(1)由题意知,抛物线的对称轴:x=1;
设OA=x,则OB=3OA=3x,即:A(-x,0)、B(3x,0);
由于A、B关于抛物线对称轴对称,所以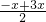 =1,即x=1,A(-1,0)、B(3,0);
=1,即x=1,A(-1,0)、B(3,0);
将B点坐标代入抛物线的解析式中,得:
0=a(3-1)2-4,解得:a=1
∴抛物线的解析式:y=(x-1)2-4=x2-2x-3.
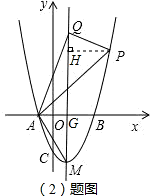 (2)设抛物线对称轴与x轴的交点为G,过P作PH⊥QM于H,如右图;
(2)设抛物线对称轴与x轴的交点为G,过P作PH⊥QM于H,如右图;
∵∠AMQ=∠PAQ,∠AGM=∠AQP=90°,
∴△AMG∽△PAQ,得: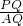 =
=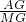 =
= ,即AQ=2PQ;
,即AQ=2PQ;
∵∠QAG=∠PQH=90°-∠AQG,∠AQP=∠PHQ=90°,
∴△AQG∽△QPH,得: =
=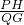 =
=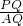 =
= ,即:QH=
,即:QH= AG=1,QG=2PH;
AG=1,QG=2PH;
设PH=x,QG=2x(x>0),则:P(x+1,2x-1),代入抛物线的解析式中,得:
(x+1)2-2(x+1)-3=2x-1,化简,得:x2-2x-3=0
解得:x=3(负值舍去);
∴P(4,5);
综上,存在符合条件的P点,且坐标为(4,5).
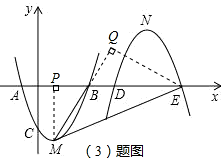 (3)过E作EQ⊥MB,交MB的延长线于点Q;过M作MP⊥x轴于P,则Rt△MPB∽Rt△EQB,得:
(3)过E作EQ⊥MB,交MB的延长线于点Q;过M作MP⊥x轴于P,则Rt△MPB∽Rt△EQB,得:
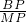 =
=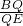 =
= ,即:QE=2BQ;
,即:QE=2BQ;
在Rt△BQE中,tan∠BME=1,则:QM=QE=2QB,即:MB=BQ;
在Rt△MPB中,PM=4,BP=2,则:MB=BQ= BP=2
BP=2 ;
;
在Rt△BQE中,QB=2 ,QE=2BQ,则:BE=
,QE=2BQ,则:BE= BQ=10,即:E(13,0);
BQ=10,即:E(13,0);
由题意知,A、E以及B、D都关于点R对称,已知:A(-1,0)、E(13,0),则:
点R的坐标为(6,0).
分析:(1)若设OA=x,则OB=3x,那么首先用x表达出A、B点的坐标,而这两点关于抛物线对称轴x=1对称,可据此确定这两点的坐标,再任取一点代入抛物线的解析式中即可求出待定系数a的值.
(2)在Rt△AOM和Rt△AQP中,有一组相等的锐角,显然这两个直角三角形是相似的,由A、M的坐标不难看出AO、OM的比例关系,可据此求出PQ、AQ的比例关系;过P作PH⊥QM于H,显然有相似三角形:△PHQ、△AQP,那么也就知道了QH、AQ以及PH、QG的比例关系(设G为抛物线对称轴和x轴的交点),首先设出PH的长,再用这个未知数表示出QG的长,即可表达出P点坐标,再代入抛物线解析式中求解即可.
(3)由于两个抛物线的对称点在x轴上,那么可视作A、E以及B、D都关于点R对称,若求R点的坐标,则必须求出点E的坐标;过E作EQ⊥MB,交MB的延长线于Q,然后过M作MP⊥x轴于P,这样就构建出了相似三角形:△MPB和△EQB,易知MP=2PB,显然有QE=2QB,而tan∠BME=1,即QE=MQ,显然有QE=MQ=2BQ,即MB=BQ,而MB的长容易求得,由此可得出BQ的长,在Rt△BQE中,由勾股定理不难求出BE的长,则E点坐标可得,题目可解.
点评:此题主要考查了二次函数解析式的确定、旋转图形的性质以及相似三角形的应用等重要知识点;后两题的难度较大,通过辅助线作出与题目相关的相似三角形是打开解题思路的关键.
设OA=x,则OB=3OA=3x,即:A(-x,0)、B(3x,0);
由于A、B关于抛物线对称轴对称,所以
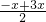 =1,即x=1,A(-1,0)、B(3,0);
=1,即x=1,A(-1,0)、B(3,0);将B点坐标代入抛物线的解析式中,得:
0=a(3-1)2-4,解得:a=1
∴抛物线的解析式:y=(x-1)2-4=x2-2x-3.
 (2)设抛物线对称轴与x轴的交点为G,过P作PH⊥QM于H,如右图;
(2)设抛物线对称轴与x轴的交点为G,过P作PH⊥QM于H,如右图;∵∠AMQ=∠PAQ,∠AGM=∠AQP=90°,
∴△AMG∽△PAQ,得:
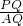 =
=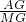 =
= ,即AQ=2PQ;
,即AQ=2PQ;∵∠QAG=∠PQH=90°-∠AQG,∠AQP=∠PHQ=90°,
∴△AQG∽△QPH,得:
 =
=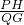 =
=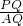 =
= ,即:QH=
,即:QH= AG=1,QG=2PH;
AG=1,QG=2PH;设PH=x,QG=2x(x>0),则:P(x+1,2x-1),代入抛物线的解析式中,得:
(x+1)2-2(x+1)-3=2x-1,化简,得:x2-2x-3=0
解得:x=3(负值舍去);
∴P(4,5);
综上,存在符合条件的P点,且坐标为(4,5).
 (3)过E作EQ⊥MB,交MB的延长线于点Q;过M作MP⊥x轴于P,则Rt△MPB∽Rt△EQB,得:
(3)过E作EQ⊥MB,交MB的延长线于点Q;过M作MP⊥x轴于P,则Rt△MPB∽Rt△EQB,得: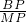 =
=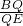 =
= ,即:QE=2BQ;
,即:QE=2BQ;在Rt△BQE中,tan∠BME=1,则:QM=QE=2QB,即:MB=BQ;
在Rt△MPB中,PM=4,BP=2,则:MB=BQ=
 BP=2
BP=2 ;
;在Rt△BQE中,QB=2
 ,QE=2BQ,则:BE=
,QE=2BQ,则:BE= BQ=10,即:E(13,0);
BQ=10,即:E(13,0);由题意知,A、E以及B、D都关于点R对称,已知:A(-1,0)、E(13,0),则:
点R的坐标为(6,0).
分析:(1)若设OA=x,则OB=3x,那么首先用x表达出A、B点的坐标,而这两点关于抛物线对称轴x=1对称,可据此确定这两点的坐标,再任取一点代入抛物线的解析式中即可求出待定系数a的值.
(2)在Rt△AOM和Rt△AQP中,有一组相等的锐角,显然这两个直角三角形是相似的,由A、M的坐标不难看出AO、OM的比例关系,可据此求出PQ、AQ的比例关系;过P作PH⊥QM于H,显然有相似三角形:△PHQ、△AQP,那么也就知道了QH、AQ以及PH、QG的比例关系(设G为抛物线对称轴和x轴的交点),首先设出PH的长,再用这个未知数表示出QG的长,即可表达出P点坐标,再代入抛物线解析式中求解即可.
(3)由于两个抛物线的对称点在x轴上,那么可视作A、E以及B、D都关于点R对称,若求R点的坐标,则必须求出点E的坐标;过E作EQ⊥MB,交MB的延长线于Q,然后过M作MP⊥x轴于P,这样就构建出了相似三角形:△MPB和△EQB,易知MP=2PB,显然有QE=2QB,而tan∠BME=1,即QE=MQ,显然有QE=MQ=2BQ,即MB=BQ,而MB的长容易求得,由此可得出BQ的长,在Rt△BQE中,由勾股定理不难求出BE的长,则E点坐标可得,题目可解.
点评:此题主要考查了二次函数解析式的确定、旋转图形的性质以及相似三角形的应用等重要知识点;后两题的难度较大,通过辅助线作出与题目相关的相似三角形是打开解题思路的关键.

练习册系列答案
相关题目
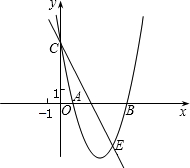 已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点. 已知:如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0)与y轴相交于点C(0,3),
已知:如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0)与y轴相交于点C(0,3), 已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.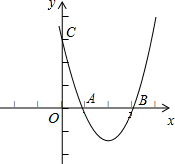 已知:如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0)与y轴相交于点C(0,3),
已知:如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0)与y轴相交于点C(0,3),