题目内容
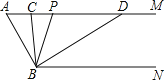
【题目】如图:已知AD平分∠BAC,∠B+∠C=180°

(1)如图①,当∠B=90°时,求证:DB=DC;
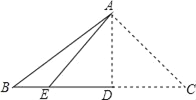
(2)如图②,如果∠ABD<90°时,(1)中的结论还成立吗?如果成立,请给出证明,如果不成立,请举反例说明;
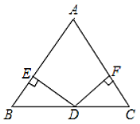
(3)如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=1,则ABAC=___.
【答案】(1)见解析;(2)成立,理由见解析;(3)![]()
【解析】
(1)利用HL判断出△ADC≌△ADC,即可得出结论;
(2)先构造出△ACD≌△AED,得出DC=DE,∠AED=∠C,在判断出DE=DB,即可得出结论;
(3)利用(2)结论得出DE=DB,再判断出∠BDE=90°,利用勾股定理求出BE即可得出结论.
(1)∵∠B+∠C=180°,∠B=90°,
∴∠C=90°.
∵AD平分∠BAC,
∴∠DAC=∠BAD,
∵AD=AD,
∴△ACD≌△ABD(AAS),
∴BD=CD;
(2)BD=CD仍成立,
理由如下:如图②,在AB边上取点E,使AC=AE,
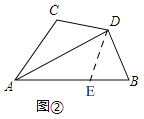
∵AD平分∠BAC,
∴∠CAD=∠EAD.
∵AD=AD,AC=AE,
∴△ACD≌△AED,
∴DC=DE,∠AED=∠C.
∵∠C+∠B=180°,∠AED+∠DEB=180°,
∴∠DEB=∠B,
∴DE=DB,
∴DB=DC;
(3)如图③,在AB上取一点E使AE=AC,

同(2)的方法得,AE=AC,CD=DE=BD=1,
∴∠DEB=∠B=45°,
∴∠BDE=90°,
根据勾股定理得,BE=![]() ,
,
∴AB-AC=BE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目