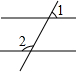题目内容
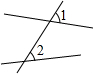
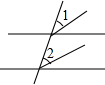
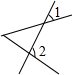
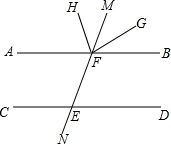
如图，AB与MN交于F，FG平分∠MFB，FH平分∠AFG，CD与MN交于E，若∠BFG：∠HFM=1：3，∠CEM=140°．
求证：AB∥CD．
求证：AB∥CD．
证明：∵FG平分∠MFB，FH平分∠AFG，
∴∠AFH=∠HFG，∠GFB=∠GFM，
∵∠BFG：∠HFM=1：3，
∴设∠GFB=x°，∠HFM=3x°，则∠MFG=x°，∠AFH=4x°，
4x+4x+x=180°，
解得：x=20，
∴∠AFM=7x°=140°，
∵∠CEM=140°，
∴∠AFM=∠CEF，
∴AB∥CD．
∴∠AFH=∠HFG，∠GFB=∠GFM，
∵∠BFG：∠HFM=1：3，
∴设∠GFB=x°，∠HFM=3x°，则∠MFG=x°，∠AFH=4x°，
4x+4x+x=180°，
解得：x=20，
∴∠AFM=7x°=140°，
∵∠CEM=140°，
∴∠AFM=∠CEF，
∴AB∥CD．
练习册系列答案
阅读快车系列答案
相关题目
