题目内容
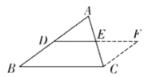
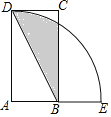
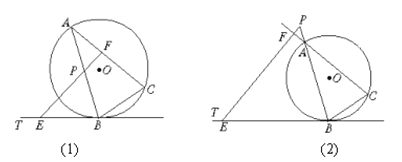
【题目】已知:△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过P作BC的平行线交直线BT于点E,交直线AC于点F.
(1)如图 (1)所示,当P在线段AB上时,求证:PA·PB=PE·PF;
(2)如图 (2)所示,当P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
【答案】(1)证明见解析;(2)对谁成立,证明见解析
【解析】
(1)利用圆周角、弦切角间的关系证明△APF∽△BPE,根据相似三角形的性质证明 PAPB=PEPF 成立.
(2)当点P在线段BA的延长线上时,(1)的结论仍成立.先证明∠AFP=∠PBE,再由∠BPE=∠FPA,可得△PAF∽△PEB,根据成比例线段证明 PAPB=PEPF 成立.
证明:(1) 如图1,连接![]() 延长
延长![]() 与圆交于
与圆交于![]()
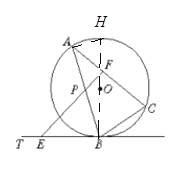
∵EB为⊙O的切线,
![]()
![]() 为⊙O的直径,
为⊙O的直径,
![]()
![]()
![]()
![]()
∴∠ACB=∠ABE,
∵EF∥BC,
∴∠AFP=∠ACB,
故∠AFP=∠ABE.
![]() ∠APF=∠EPB,
∠APF=∠EPB,
∴△APF∽△BPE,
![]()
∴PAPB=PEPF.
(2)结论成立,理由如下:
∵EB为⊙O的切线,结合(1)问:
∴∠ACB=∠ABT,
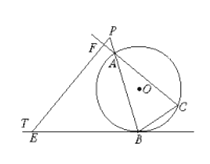
∵EF∥BC,
∴∠ACB =∠AFP,
![]()
∴∠AFP=∠PBE.
![]() ∠BPE=∠FPA,
∠BPE=∠FPA,
![]() △PAF∽△PEB,
△PAF∽△PEB,
![]()
∴PAPB=PEPF.
当点P在线段BA的延长线上时,(1)的结论仍成立.

【题目】某旅行团计划今年暑假组织一个老年人团去昆明旅游,预定宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准为每人每天120元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的,超出部分按八折收费.设老年团的人数为![]() .
.
(1)根据题意,用含有![]() 的式子填写下表:
的式子填写下表:
|
|
|
| |
甲宾馆收费/元 |
| 5280 | ||
乙宾馆收费/元 |
|
| 5400 |
(2)当老年人团的人数为何值时,在甲、乙两家宾馆的花费相同?如果老年人团的人数超过60人,在哪家宾馆住宿比较省钱?