题目内容
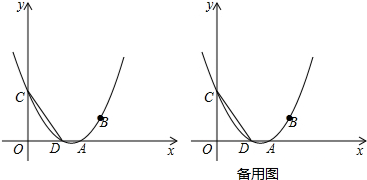
(2013•鞍山二模)已知:在△ACB中,∠ACB=90°,CD⊥AB于D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F,
(1)如图1,AC=BC,点E为AC的中点,求证:EF=EG;
(2)如图2,
=
,AC=2BC,试探究∠CBE与∠ABE的关系,并证明你的结论.
(1)如图1,AC=BC,点E为AC的中点,求证:EF=EG;
(2)如图2,
| EF |
| EG |
| ||
| 2 |

分析:(1)作EM⊥AB于点M,EN⊥CD于点N,根据全等三角形的证明方法利用ASA得出△EFM≌△EGN,即可得出EF=EG;
(2)∠CBE=∠ABE,作EP⊥AB于点P,EQ⊥CD于点Q,易证△EFP∽△EGQ,利用相似三角形的性质和已知条件证明EP=CP即可.
(2)∠CBE=∠ABE,作EP⊥AB于点P,EQ⊥CD于点Q,易证△EFP∽△EGQ,利用相似三角形的性质和已知条件证明EP=CP即可.
解答: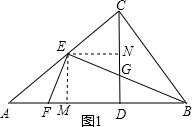 证明:(1)如答图1,过E作EM⊥AB于M,EN⊥CD于N,
证明:(1)如答图1,过E作EM⊥AB于M,EN⊥CD于N,
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴AD=CD,
∵点E为AC的中点,CD⊥AB,EN⊥DC,
∴EN=
AD,
∴EM=
CD,
∴EN=EM,
∵∠FEB=90°,∠MEN=90°,
∴∠NEG=∠FEM,
在△EFM和△EGN中,
,
∴△EFM≌△EGN(ASA),
∴EF=EG;
(2)解:∠CBE=∠ABE,
理由如下: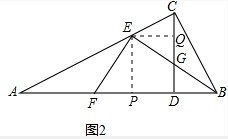
作EP⊥AB于点P,EQ⊥CD于点Q,
易证:△EFP∽△EGQ,
∴
=
=
,
设EP=
x,QE=2x,
∵∠A=CEQ,
∴tan∠CEQ=
=tanA=
=
,
∴CQ=x,∴CE=
x,
∴EP=EC,
∵EP⊥AB于点P,EC⊥CB于C,
∴∠ABE=CBE.
 证明:(1)如答图1,过E作EM⊥AB于M,EN⊥CD于N,
证明:(1)如答图1,过E作EM⊥AB于M,EN⊥CD于N,∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°,
∴AD=CD,
∵点E为AC的中点,CD⊥AB,EN⊥DC,
∴EN=
| 1 |
| 2 |
∴EM=
| 1 |
| 2 |
∴EN=EM,
∵∠FEB=90°,∠MEN=90°,
∴∠NEG=∠FEM,
在△EFM和△EGN中,
|
∴△EFM≌△EGN(ASA),
∴EF=EG;
(2)解:∠CBE=∠ABE,
理由如下:

作EP⊥AB于点P,EQ⊥CD于点Q,
易证:△EFP∽△EGQ,
∴
| EF |
| EG |
| EP |
| EQ |
| ||
| 2 |
设EP=
| 5 |
∵∠A=CEQ,
∴tan∠CEQ=
| CQ |
| EQ |
| BC |
| AC |
| 1 |
| 2 |
∴CQ=x,∴CE=
| 5 |
∴EP=EC,
∵EP⊥AB于点P,EC⊥CB于C,
∴∠ABE=CBE.
点评:此题主要考查了全等三角形的判定与性质、相似三角形的判定与性质、角平分线性质定理的逆定理以及锐角三角函数的概念的考查.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
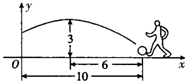 (2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
(2013•鞍山二模)在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.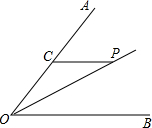 (2013•鞍山二模)如图,∠AOP=∠BOP,CP∥OB,CP=4,则OC=( )
(2013•鞍山二模)如图,∠AOP=∠BOP,CP∥OB,CP=4,则OC=( )