题目内容
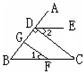20、如图，CD⊥AB于D，DE∥BC，∠1=∠2．你能说明FG⊥AB吗？为什么？分析：先根据两直线平行，内错角相等得到∠C=∠2，所以∠1=∠C，所以CD∥FG，又CD⊥AB，所以FG⊥AB．
解答：解：FG⊥AB．
∵DE∥BC，
∴∠2=∠C（两直线平行，内错角相等）．
∵∠1=∠2，
∴∠1=∠C，
∴CD∥FG（同位角相等，两直线平行）．
又∵CD⊥AB，
∴FG⊥AB．
∵DE∥BC，
∴∠2=∠C（两直线平行，内错角相等）．
∵∠1=∠2，
∴∠1=∠C，
∴CD∥FG（同位角相等，两直线平行）．
又∵CD⊥AB，
∴FG⊥AB．
点评：本题是平行线的性质和判定定理的综合运用，是基础题，需要熟练掌握．
练习册系列答案
相关题目
25、已知如图，CD⊥AB于D，EF⊥AB于F，∠1=∠2，请问DG∥BC吗？如果平行，请说明理由．
23、已知：如图，CD⊥AB于D，点E为BC边上的任意一点，EF⊥AB于F，且∠1=∠2，那么BC与DG平行吗？请说明理由．
17、如图，CD⊥AB于E，若∠B=60°，则∠A=
18、如图，CD⊥AB于D，DE∥BC，∠1=∠2，则FG与AB的位置关系是
如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠3=∠BCA，那么∠1与∠2有什么关系？请说明理由．