题目内容
观察下列等式：
；
；
；
；
… …
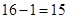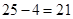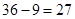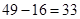用自然数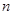
（其中
）表示上面一系列等式所反映出来的规律是 ．
；；；；… …
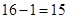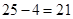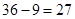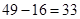用自然数
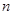（其中）表示上面一系列等式所反映出来的规律是 ．（n+3）2﹣n2=6n+9．
等式的左边是两个平方项的差，且第一个平方项比第二个平方项多3，所以左边表示为（n+3）2﹣n2.利用平方差公式（n+3）2﹣n2=（n+3-n）（n+3+n）=3（2n+3）=6n+9.
练习册系列答案
名校课堂系列答案
相关题目
，
，
，
，
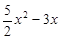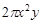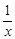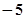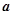中，单项式的个数是 
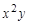是同类项的是（ ）
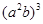的结果是
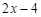的值为5，那么
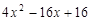的值是 ．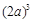 
＝ ．
．
；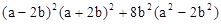