题目内容
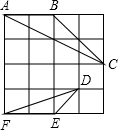 (1)如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
①填空:∠ABC=______°;∠DEF=______°;BC=______;DE=______;
②判断△ABC与△DEF是否相似,并证明你的结论.
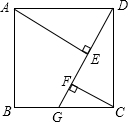
(2)如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.求证:△ADE≌△DCF.
(1)解:①135°,135°,2 ,
, ;
;
②△ABC与△DEF相似.
理由:由图可知,AB=2,EF=2
∴ =
= .
.
∵∠ABC=∠DEF=135°,
∴△ABC∽△DEF.
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADG+∠CDG=90°.
又∵AE⊥DG,
∴∠AED=∠AEF=90°,
∴∠DAE+∠ADE=90°,
∴∠DAE=∠CDG.
∵CF∥AE,
∴∠CFD=∠AEG=90°,
∴∠AED=∠CFD.
∴△ADE≌△DCF.
(注:如果有不同的解题方法,只要正确,可参考评分标准,酌情给分.)
分析:(1)①因为BC、DE是正方形的对角线,根据正方形对角线平分对角计算角度;根据勾股定理求长度.②证明两边对应成比例,且夹角相等判定相似.
(2)AE⊥DG,CF∥AE,则∠AED=∠DFC=90°;∠CDF+∠ADE=90°,∠ADE+∠DAE=90°,则∠CDF=∠DAE.两角对应相等则相似.
点评:此题考查了相似三角形的判定和性质.问题(1)是网格问题,要求学生有较强的分析能力,难度偏上.
 ,
, ;
;②△ABC与△DEF相似.
理由:由图可知,AB=2,EF=2
∴
 =
= .
. ∵∠ABC=∠DEF=135°,
∴△ABC∽△DEF.
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADG+∠CDG=90°.
又∵AE⊥DG,
∴∠AED=∠AEF=90°,
∴∠DAE+∠ADE=90°,
∴∠DAE=∠CDG.
∵CF∥AE,
∴∠CFD=∠AEG=90°,
∴∠AED=∠CFD.
∴△ADE≌△DCF.
(注:如果有不同的解题方法,只要正确,可参考评分标准,酌情给分.)
分析:(1)①因为BC、DE是正方形的对角线,根据正方形对角线平分对角计算角度;根据勾股定理求长度.②证明两边对应成比例,且夹角相等判定相似.
(2)AE⊥DG,CF∥AE,则∠AED=∠DFC=90°;∠CDF+∠ADE=90°,∠ADE+∠DAE=90°,则∠CDF=∠DAE.两角对应相等则相似.
点评:此题考查了相似三角形的判定和性质.问题(1)是网格问题,要求学生有较强的分析能力,难度偏上.

练习册系列答案
相关题目
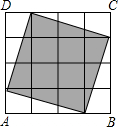 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )| A、5:8 | B、3:4 | C、9:16 | D、1:2 |
 如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是( )
如图,在等腰三角形ABC中,∠ABC=120°,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM+PN的最小值为2,则△ABC的周长是( ) 12、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )
12、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )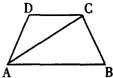 19、如图,在梯形ABCD中,DC∥AB,AD=BC,AC平分∠DAB,∠DCA=30°,DC=3厘米,则梯形ABCD的周长为
19、如图,在梯形ABCD中,DC∥AB,AD=BC,AC平分∠DAB,∠DCA=30°,DC=3厘米,则梯形ABCD的周长为 若不是,请说明理由;
若不是,请说明理由;