Question

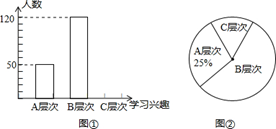
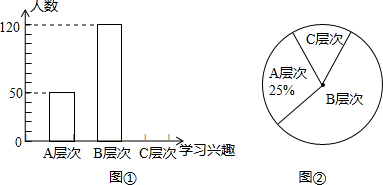
学生的学习兴趣如何是每位教师非常关注的问题．为此，某校教师对该校部分学生的学习兴趣进行了一次抽样调查（把学生的学习兴趣分为三个层次，A层次：很感兴趣；B层次：较感兴趣；C层次：不感兴趣）；并将调查结果绘制成了图①和图②的统计图（不完整）．请你根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了______名学生；
（2）图①、②补充完整；
（3）将图②中C层次所在扇形的圆心角的度数；
（4）根据抽样调查的结果，请你估计该校1200名学生中大约有多少名学生对学习感兴趣（包括A层次和B层次）．

Answer 1

解：（1）此次抽样调查中，共调查了
50÷25%=200（人）；
故答案为：200．

（2）C层次的人数为：200-120-50=30（人）；
所占的百分比是：×100%=15%；
B层次的人数所占的百分比是1-25%-15%=60%；

（3）C层次所在扇形的圆心角的度数是：360×15%=54°；

（4）根据题意得：
（25%+60%）×1200=1020（人）
答：估计该校1200名学生中大约有1020名学生对学习感兴趣．
分析：（1）由A层次的人数所占比例为25%，A层次人数为50，故调查总人数为50÷25%=200；
（2）根据调查总人数为200，故C层次的人数为200-120-50=30；B层次的人数所占的百分比是1-25%-15%；
（3）C层次所在扇形的圆心角的度数可通过360°×15%求得；
（4）由样本中A层次和B层次所占比例为60%和25%，所以可以估计对学习感兴趣的人数．
点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．